Improving a policy →
In a previous post we evaluated a given policy $\pi$ by computing the state value function $v_{\pi}(s)$ in each of the states of the system. In this post, we will start with a random policy, use the function policy_eval() developed in the previous post to improve the random policy we started with and end up in an improved policy as a result.
Recall from a previous post the intuition behind action value function.
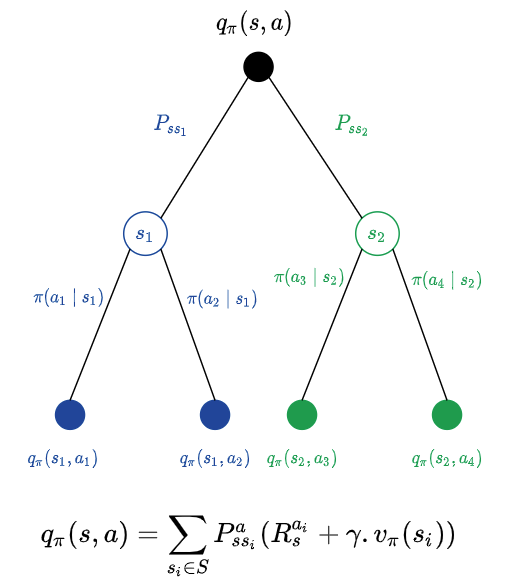
Our goal now is to do a one step lookahead and calculate the action values for different possible actions and pick the action that would fetch us the maximum action value. The following function follows the equation in the sketch above and computes action values for different possible actions.
def one_step_lookahead(env, st, v, gamma=0.9):
action_values = np.zeros(env.action_space.n)
for a in range(env.action_space.n):
for nxt_st_prob, nxt_st, reward, done in env.P[st][a]:
action_values[a] += nxt_st_prob * (reward + gamma * v[nxt_st])
return action_values
Here is what we are going to do:
- Start with a random policy
- Evaluate the policy (using
policy_eval()) and get the state values for all the states - Take one step (using
one_step_lookahead()) and take the action that maximizes the action value (greedy step) and then follow our usual policy for the rest of the episode - Return the updated state values (resulting from one step of greedy action) along with the policy (better policy)
action_values = one_step_lookahead(env, s, v)
best_a = np.argmax(action_values)
action_values is a 4 element array (as there are four actions - Up, Down, Right and Left). The array indices indicate the action while the array elements indicate the action value ($q(s, a$)). argmax(action_values) would return the action that has the maximum action value.
Putting it all together:
def policy_iter(env, gamma=0.9, max_iter=10000):
# (1) start with random policy
policy = np.ones([env.observation_space.n, env.action_space.n]) / env.action_space.n
# policy eval counter
policy_eval_cnt = 1
# repeat until convergence or max_iter
for i in range(int(max_iter)):
stop = False
# (2) evaluate current policy
v = policy_eval(policy, env)
for s in range(env.observation_space.n):
# current action according to our policy
curr_a = np.argmax(policy[s])
# (3) look one step ahead and check if curr_a is the best
action_values = one_step_lookahead(env, s, v)
# select best action greedily from action_values from one-step lookahead
best_a = np.argmax(action_values)
if (curr_a != best_a):
stop = False
# update the policy
policy[s] = np.eye(env.action_space.n)[best_a]
else: # curr_a has converged to best_a
stop = True
policy_eval_cnt += 1
if (stop):
# (4) return state values and updated policy
return policy, v
This is referred to as Policy Iteration as we iteratively improve the policy that we started with, evaluating the policy in each iteration.