In a previous post we saw Bellman Expectation Equation for state value function $v_{\pi}(s)$. Following similar derivations, we can also derive Bellman Expectation Equation for the action value function $q_{\pi}(s, a)$.

Action value function $q_{\pi}(s, a)$ that denotes how good is it to take an action $a$ while being in state $s$

\[q_{\pi}(s, a) = \mathbb{E}_{\pi}[G_t \mid S_t = s, A_t = a]\]

Since we know, from an earlier post that the return $G_t$ is the total discounted rewards starting from state s.

\[G_t = R_{t+1} + \gamma R_{t+2} + \cdots = \sum_{i=0}^{\infty} \gamma^{i} R_{t+i+1}\]

Using the above in $q_{\pi}(s, a)$,

\[q_{\pi}(s, a) = \mathbb{E}_{\pi}[R_{t+1} + \gamma q_{\pi}(S_{t+1}, A_{t+1}) \mid S_t = s, A_t = a]\]

Given a policy $\pi$, how good the action $a_1$ is would be known only by evaluating the action value function $q_{\pi}(s, a_1)$ for action $a_1$ while in state s , very analogous to evaluating the state value function $v_{\pi}(s)$ to evaluate how good the state s is. Suppose we have commited to an action a, the environment could react and take us to different states. Recall the earlier example, where we could have invested $300 in the stock market and the environment could have taken us to a state beneficial to us or to a state of despair. Formally, there could be different transitions possible out of our current state, with different transition probabilities, leading to different states. For example, an action a from state s could take us to state $s_1$ with probability $P_{ss_1}^{a}$ or to state $s_2$ with probability $P_{ss_2}^{a}$. When we are at a state where we have committed the action ($300 invested in stock) represented by the black filled circle, the value of the action would be the average of all the transition dynamics (as we do not know how the environment would react, yet).


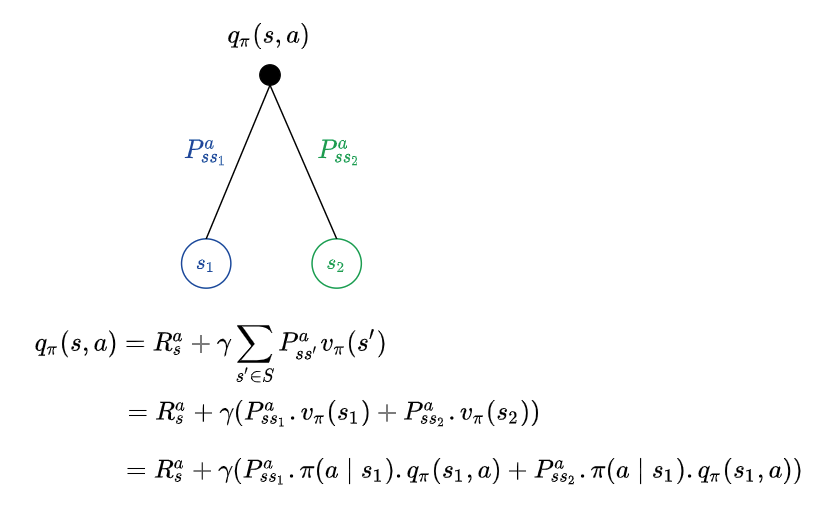
Putting the state value function and action value function together,


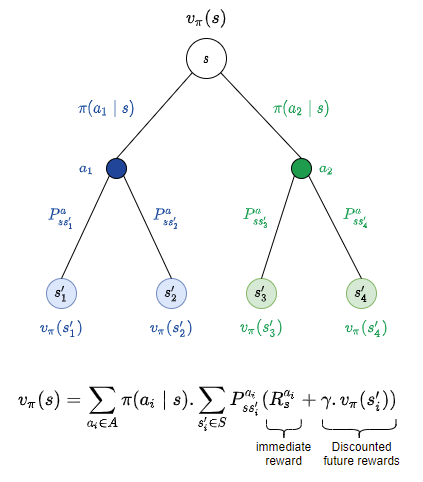
Similarly, we could put the action value function and state value function together, as below.


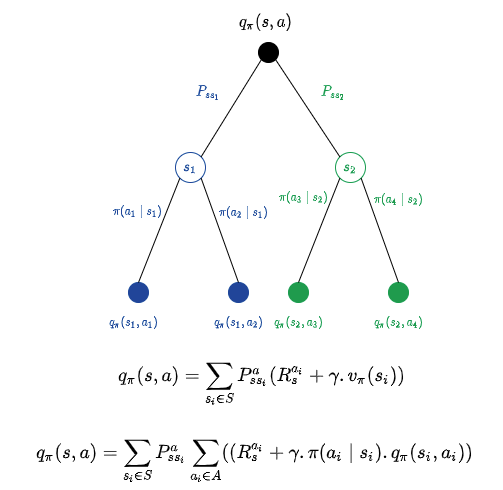
This might look like lot many equations, but when we write an algorithm to implement these, we would use the equations as it is and hence these are very important to be understood.