Evaluating a policy →
In one of the previous posts we saw how to evaluate the value of a state s $v_{\pi}(s)$. In this post, we will try to implement it using OpenAI Gym. Let us recall the following image that would help us in writing our policy evaluation function.
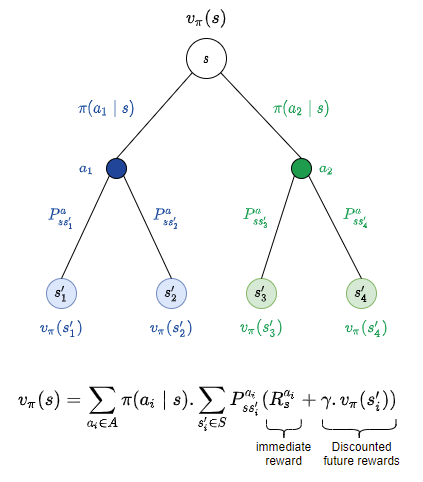
The main goal of policy evaluation is to find the state value function of the states in the system, given a policy $\pi$. To recap, for a given state $s$, there could be multiple possible actions and probabilities of each of the actions. Once we commit to an action, the environment could perform its turn of the action and our action could take us to different potential ‘next’ states, each with a probability of transition. We average over all the action probabilities $\pi(a_i \mid s)$ and over the transition probabilities $P_{ss’_{i}}^{a_i}$ and compute immediate reward and discounted rewards on next state.
The (pseudo)code fragment for the different components are given alongside the figure below for better intuition.
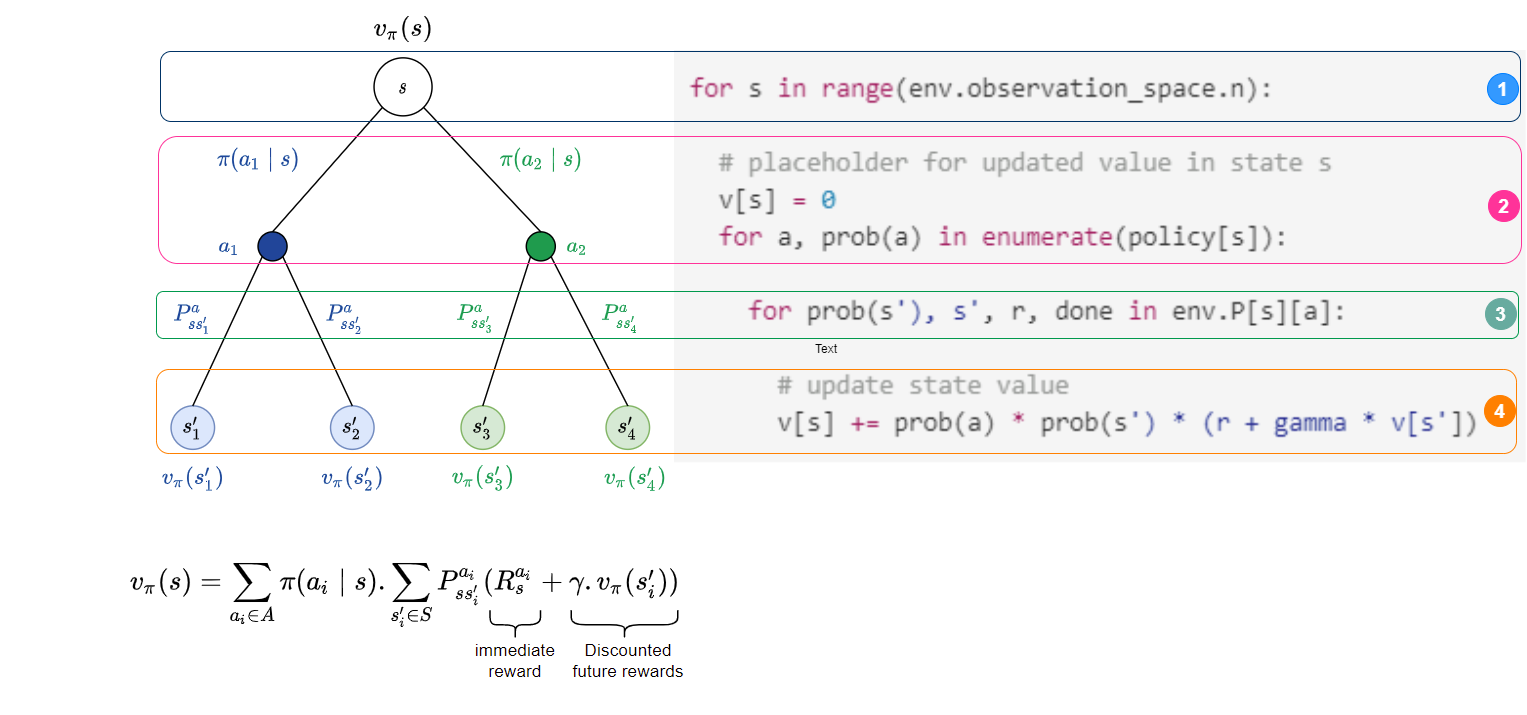
In the pseudocode above, prob(a) denotes the probability of action a (i.e. $\pi(a \mid s)$), s’ denotes the possible next state, and prob(s') denotes the transition dynamics (i.e. $P^{a}_{ss’}$).
Putting the above together in code:
def policy_eval(policy, env, gamma=0.9, th=1e-9, max_iter=10000):
# number of iterations of evaluation
eval_iter = 1
# initialize the value function for each state
v = np.zeros(env.observation_space.n)
# repeat update until change in value is below th
for i in range(int(max_iter)):
# initialize change in value to 0
delta = 0
# for each state in env
for st in range(env.observation_space.n):
# initialize new value of current state
v_new = 0
# for each state s,
# v_new(s) = E[R_t+1 + gamma * V[s']]
# average over all possible actions that can be taken from st
for a, a_prob in enumerate(policy[st]):
# v_new(s) = Sum[a_prob * nxt_st_prob * [r + gamma * v[s']]]
# check how good the next_st is
for nxt_st_prob, nxt_st, reward, done in env.P[st][a]:
# calculate bellman expectation
v_new += a_prob * nxt_st_prob * (reward + gamma * v[nxt_st])
# check to see if new state is better
delta = max(delta, np.abs(v[st] - v_new))
# update V
v[st] = v_new
eval_iter += 1
# if value change is < th, terminate
if delta < th:
return v
The above function has some more details. It iteratively does it for a given max_iter number of iterations. Further, there is also an input threshold th which is used to decide when to stop updating the state value function v, by measuring the difference (delta) between the existing value and new value until it is negligible (as defined by th).