In an earlier post, we saw implementation of Queues using arrays. Now, we will use a Linked List to store the elements instead of an array. Since we are all linked list champs by now, we already know how to go about building a linked list given an input set of elements - create nodes that contain our elements and join the nodes using next pointers.

We will also use this example to introduce the notion of a friend class in C++.

A friend class F is a C++ class that can access private and protected members of another class A in which F is declared as friend. Here, a Queue class (F) may be allowed to access private members of a Node class (A).

class Node {
  private:
    int data;
    Node *next;
    friend class Queue;
};

class Queue {
  private:
    Node *front, *rear;
  public:
    Queue ();
    void enqueue (int item);
    bool is_empty ();
    int dequeue ();
};

Queue::Queue () {
  this->front = NULL;
  this->rear = NULL;
}

There is also a notion of friend function, very similar to friend class:

A friend function f can be used to access private and protected members of a class A and it can be either:

• a method of a class A
• a global function

In the following post, we will see how to implement the methods enqueue() and dequeue() for the Queue class above.

In our previous post, we looked at the modelling of the Queue class using an array as the container to hold the queue elements. front and rear indicate the boundary of the queue (the first and the last elements). When we want to add a new element, we add it at the rear. Likewise, when we want to remove and process an element, we remove it from the front. That is, enqueue increments the rear member and dequeue increments the front member.

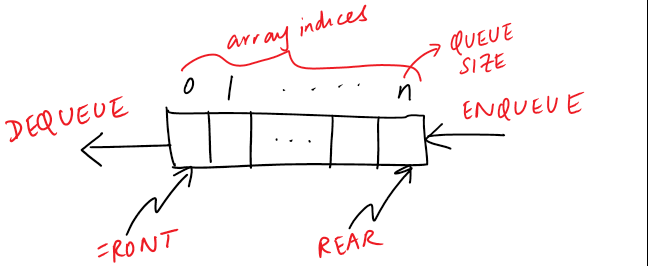
void Queue::enqueue (int item) {
  if (rear >= MAXSIZE - 1)
    throw out_of_range("Queue is full. Nothing can be enqueued now.");
  else {
    arr[++rear] = item;
  }
}

int Queue::dequeue () {
  if (rear == -1)
    throw out_of_range("Can not dequeue from empty queue");
  return arr[front++];
}

So, when front = rear there is only one element and if front > rear, the queue is empty (recollect that the front is initialized to 0 and rear is initialized to -1).

bool Queue::is_empty () {
  return (front > rear);
}

Although pretty straight-forward, Queues have a variety of applications. We will soon see some applications when we discuss Graph data structures.

Let’s look at another important data structure - the Queue. As the name indicates, it is used just to model a queue of objects. The collection of objects in the queue will be served (or processed) much like how a queue of people in front of a ticket vending counter are served - the first one in the queue gets served first, and the last one in the queue gets served last. This kind of system is more popularly called FIFO (for First-In-First-Out system). Queue, is just a collection of objects - which means we can use an array to model them (to hold the objects) or alternatively we could also use a linked list (which also just holds a collection of objects). The operations on those objects should follow the FIFO order, while the container itself could be anything. Let use first model it using an array:

#define MAXSIZE 100
class Queue {
  private:
    int front, rear;
    int arr[MAXSIZE];
  public:
    Queue ();
    void enqueue (int item);
    int dequeue ();
    bool is_empty ();
};

Queue::Queue () {
  front = 0;
  rear = -1;
}

We have two private members - front and rear - front gets served first. Objects get added to the container using the enqueue() method and they get processed in FIFO order using dequeue() method. We will look at these operations in future posts.

In our previous post, we looked at an iterative function to reverse a linked list. I believe it was a lot of fun. Now, we shall look at a recursive function to do the same. As before, whenever you hear recursion, you should just think of the base case and the recursive steps (i.e. what is to be done in each recursive step - like printing the node’s data in our recursive print function) - once this is clear, the rest would be straight forward. For reversing a linked list, at each recursive step, we need to update the pointer directions - if there is a pointer C --> D, after the recursive call it would be C <-- D. We keep track of two pointers, head and rest (everything following head) - and recursively call the function.

void LinkedList::reverse_list_r () {
  Node *rest = NULL;
  Node *first = NULL;
  first = this->head;
  rest = first->next;
  if (first == NULL || rest == NULL)
    return;                   // base case
  this->head = rest;          // move forward
  this->reverse_list_r ();    // recursive call  
  rest->next = first;         // update pointers
  first->next = NULL;
}

I will leave it as an (interesting) exercise for the reader to work out this function as we did for the iterative case.

In this post, let us try to write a function to reverse our linked list. In particular, we will do it in an iterative fashion. Suppose we start with the following input list:

1  -->  2  -->  3  -->  NULL

After performing a reversal we should end up with the following result:

3  -->  2  -->  1  -->  NULL

Conceptually, we are reversing the pointers (turing around the arrows). In our data structure, these are denoted by the next pointer of each node. So, it is actually just setting the next pointer of the current node to point to the previous node in the list. For example, if our current node is 2 and its next pointer is pointing to node 3 originally, we want our function to make the next pointer of 2 to point to 1. We are remembering the previous node just as in our previous example to delete a node. It looks like that’s all to it:

curr->next = prev

But as soon as we set the next pointer of 2 to point to 1, we lost the connection to the rest of the list following 2 (3 --> NULL). Intuitively, to get over this, we need to remember more than just the previous node in the list - we also need to keep track of the next node (a handle to the next node so that we do not lose the rest of the list after we turn the current node’s next pointer). Once you have a grasp of this intuition the coding it up is straight-forward. For better clarity, let us also work through a simple example (with 3 elements as above) following the function definition below:

void LinkedList::reverse_list () {
  Node *prev = NULL;
  Node *next;
  Node *curr = this->head;
  while (curr != NULL) {
    next = curr->next; // get the next element
    curr->next = prev; // link in reverse direction 
    prev = curr;       // move ahead - set new prev, curr  
    curr = next;
  }
  this->head = prev;
}

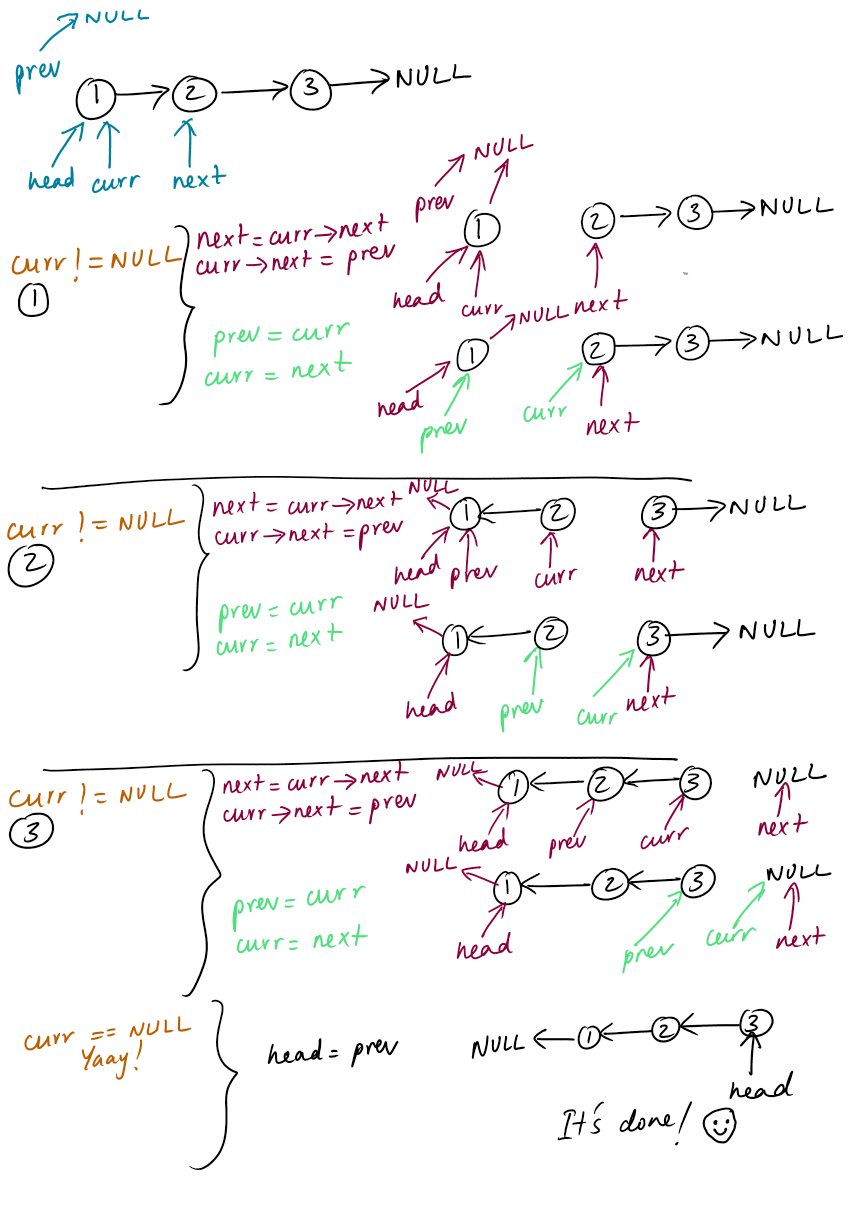
Now, you get it!