String subsequences - Extracting the LCS →
In the previous post we saw how to compute the length of the longest common subsequence (LCS). The algorithm returned an integer value indicating the length of the LCS. How do we go about extracting the LCS? With a simple extension to the previous algorithm, we can also extract the string sequence that is the LCS. In particular, we will traverse the populated lookup table and extract the LCS from that.
Let us consider a simple example, so that we can work it out by hand. Let the string s1 be ABCD and string s2 be BAD. Once we populate the lookup table as shown previously, it would look something like the one below

Populating the lookup table is the same as in our previous post, with just a reference to our lookup table passed to our function.
void lcs_dp(std::string s1, std::string s2, int m, int n,
std::vector<std::vector<int>>& lookup)Note that when either of the strings is empty, LCS is also empty and hence the length of the LCS is 0.
If one observes the LCS algorithm carefully, when a character of the strings match, in order to compute the value at (i, j) we look at the smaller subproblem (diagonally above and to the left - at coordinates (i-1, j-1) and add 1 to it.
if (s1[i-1] == s2[j-1])
lookup[i][j] = lookup[i-1][j-1] + 1;This tells us that if there is a match, the character in the string s1[m-1] (or s2[n-1]) would be a part of the LCS and hence we collect it in our result string and call our processing (the lookup table) function on the rest of the table, starting at (m-1, n-1).
If there is no match, then we compute the max of the subsequence lengths from (m-1, n) and (m, n-1). Potentially these could be two subsequences with the last character (that matched) the same.
else
lookup[i][j] = std::max(lookup[i-1][j], lookup[i][j-1]);Essentially, for the value of the cell (i, j) we were computing the max of the values in the top cell (i-1, j) and the left cell (i, j-1). In order to extract the LCS, we hence need to move in the direction of the max (i.e. whether the current cell value was influenced by the top cell or the left cell).
Putting this together,
std::string get_lcs(std::string s1, std::string s2,
int m, int n,
std::vector<std::vector<int>>& lookup)
{
if (m == 0 || n == 0)
return std::string("");
if (s1[m-1] == s2[n-1])
return get_lcs(s1, s2, m-1, n-1, lookup) + s1[m-1];
int top_cell = lookup[m-1][n];
int left_cell = lookup[m][n-1];
if (top_cell > left_cell)
// go up
return get_lcs(s1, s2, m-1, n, lookup);
else
// go left
return get_lcs(s1, s2, m, n-1, lookup);
}The traversal of the lookup table extracting the LCS ad is shown below:
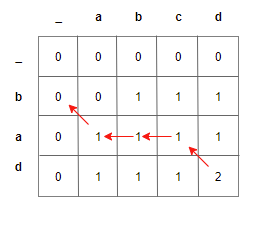
But LCS is not unique. There can be many LCS for a pair of strings. How do we collect all of the longest common subsequences?