Those who cannot remember the past are condemned to repeat it!

In our previous post we saw a recursive algorithm to compute the number of ways one can climb a fleet of n steps. If you draw the recursion tree for such an algorithm, we would soon find that we are computing some of the sub-problems repeatedly. We can do better by remembering (i.e. storing in some data structure) what we computed so that we can retrieve it and reuse it when needed again. Or in other fancy computer science parlance, we can use dynamic programming technique to solve such recursive problems more efficiently.

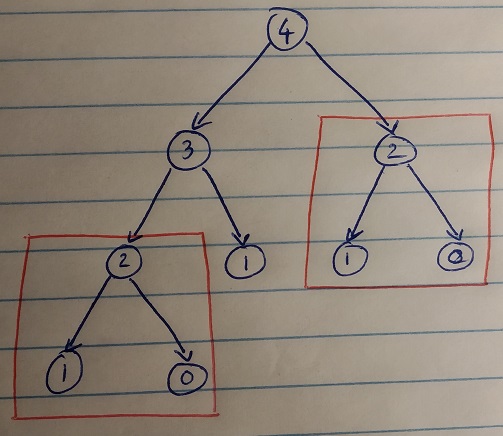
Here is the recursion tree for a hypothetical problem, similar to climbing stairs from our previous post where each function call for an input parameter value n leads to two calls for values n-1 and n-2. We can readily see, even in this very small example, that the all the function calls in the sub-tree rooted at 2 is computed again unnecessarily. One of the main ideas in dynamic programming is to store such computations so that we can reuse them when needed again.


recursion tree

Let us try to use dynamic programming and rewrite our algorithm for computing the number of ways of climbing n steps. We shall use a simple array (a C++ vector) to store intermediate computations. More concretely, we will store the number of ways of climbing 1 step, the number of ways of climbing 2 steps, and so on. So, our array ways stores the number of ways - ways[i] gives us the number of ways of climbing i steps. As we saw in our previous post, the algorithm just needs to compute ways[i-1] + ways[i-2] for different values of i upto n and finally return ways[n] as the result.

int stairs(int n)
{
  std::vector<int> ways(n+1);

  // base case
  if (n <= 1)
    return 1;

  ways[0] = 1;
  ways[1] = 1;
  for (int i = 2; i <= n; i++)
    ways[i] = ways[i-1] + ways[i-2];

  return ways[n];
}

An astute reader would start thinking how this is different from divide-and-conquer approaches for solving recursive problems. I will let you think about it for now and find out for yourself what technique is beneficial for what specific structure of the recursive problem - that was already a hint there!