In our previous post, we found a way to compute the position of the right-most set bit in a given number. A key ingredient of that algorithm was isolating the right-most set bit. For example, given 10, which is 1010 in binary, how do we “isolate the right-most set bit” - i.e. generate a bit-vector where only the bit in the position of the right-most set bit, in our input number, is set. For our input number 10, it would be a bit-vector where only the bit in position 2 is set - 0010. Given 1010, how do we generate 0010?

We mentioned about 2’s complement notation for negative numbers in a previous post. For example, the number 2 represented using 4 bits would be 0010 while -2 represented using 4 bits would be 1110, where the bit position corresponding to right-most set bit in in the positive equivalent (+2) is set, while all the bits to the left are flipped.


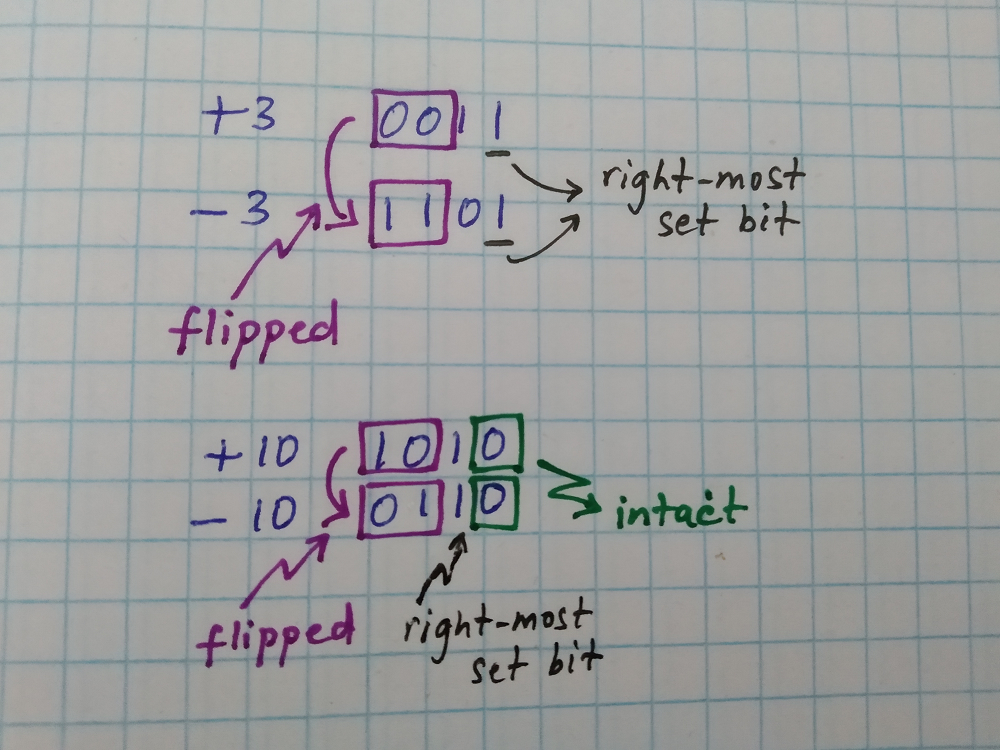
isolating right-most set bit

Now, if we & (bit-wise AND) our input number (x) with the negation of it (-x), we will be left with only one bit set, which corresponds to the position of the right-most set bit. So, the bit-wise operation we were looking for is & with the negation of the input number. Let us put all this together in a C algorithm (not that we already know the later part of the algorithm from the previous post):

int rightmost_set_bit (int x)
{
  // isolate the rightmost set bit
  x = x & (-x);
  int count = 0;
  while (x != 0)
  {
    x = x >> 1;
    count++;
  }
  return count;
}