In a previous post we saw how to write a recursive function to compute permutations of characters of a string. But we were computing redundant permutations when the input string had duplicated characters, as in the input string “AAB”. What could we do to avoid the redundant computations?

Intuitively we need to avoid some recursive calls that we know will lead to redundant computations. The sub-trees corresponding to this redundant computation are marked red in the sketch below:
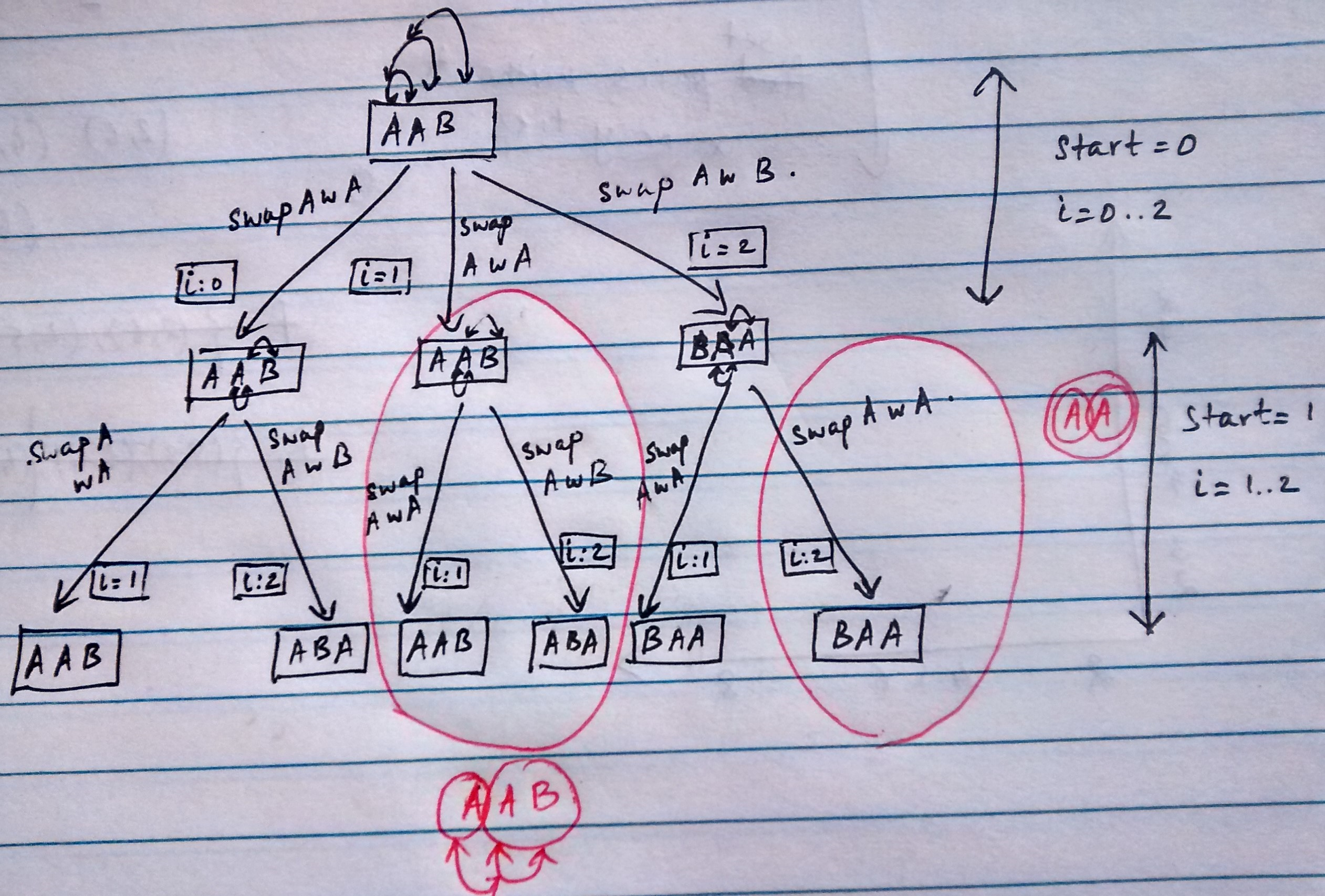
Permutations of "ABC"

What it indicates is that when we have the substring that we are processing (by walking through the characters in the substring) we look at the characters we process and decide if we want to go down that recursive path.

Let’s go through a couple of paths in the recursion tree above and try to figure this out:

  1. (start:0, i:0): The string we are staring with is AAB, substring starting at start is AAB and substring starting at i is also AAB (as i is start to begin with). Now we swap s[start] and s[i] which are both A. Now we call the _permute() with start incremented by 1. a. (start:1, i:1..2): Now the substring starting at start is AB (as start is 1) and substring starting at i is AB. Further s[start] is A and s[i] is also A. We hence perform a swap producing AAB and backtrack. Now, i:2 and so s[start] is A and s[i] is B. We swap A and B and get ABA.

  2. (start:0, i:1): The string we are staring with is AAB, substring starting at start is AAB and substring starting at i is also AB (as i is 1 now). We have substring_from_start different from substring_from_i but s[start] is the same as s[i] which means that if we do a swap, we will yield the same thing and also we would have come across this earlier as we have processed the substring corresponding to this i. So we avoid going down this path and start working through start:0, i:2.

So the condition we are looking for traversing is that substring(start) and substring(i) are same and further the starting character at start and i are the same. Further, if substring(start) and substring(i) are different and the starting characters are different, we go ahead with the traversal (as in start:0, i:2).

Here is the modified permute() function with the condition incorporated:

void permute(string s, int start, int end) {
  int i;
  if (start == end)
    cout << s << endl;
  else {
    for (i=start; i<=end; i++) {
      // handle duplicates
      if ((s.at(start) != s.at(i)) || 
          ((s.substr(start, end-start+1) == s.substr(start, end-i+1)) && 
           (s.at(start) == s.at(i)))) {
        swap(s[start], s[i]);
        permute(s, start+1, end);
        swap(s[start], s[i]);
        }
    }
  }
}

Hope you can refer to the sketch above, work through the example and feel convinced.