I don’t know how my posts just happen to revolve around recursion, but we’re only one week into learning and I have grand plans to learn (through teaching) deep learning techniques, data analysis, hardware engineering concepts, etc., besides recursion and functional programming. So, just hang on and enjoy!

Let’s do a quick example to work out more recursion. This time, we will implement selection sort. Selection sort implementation, again, is very intuitive if we are in this thought process - recursion and a terse and intuitive programming language. Let’s do it. We just need to traverse the list, select the minimum element and append it to the head of the list. And then, proceed by finding the next minimum element (from the rest-of-the-list which contains one element less than the original list as the minimum element has been moved to the head) and push it to the head, and so on. So we need two ingredients.

• A function rem to remove an element x from a list lst. We will write it in recursive fashion
• A function find_min to find the minimum element of a list (we already did this in one of our previous posts)

Let’s implement the above ingredients that we need for selection sort recipe.

let rec rem x lst =
  match lst with
  | [] -> []
  | h::t ->
     if (h = x) then t
     else h::(rem x t);;

let rec find_min lst =
  match lst with
  | [] -> failwith("empty list")
  | [x] -> x
  | h::t -> min h (find_min t);;

Now, let’s use the above two to implement selection sort. We will call the function ssort. Recollect that, we will find the minimum element m of the list, push it to the head (actually we also have to remove it from the rest-of-the-list otherwise there will be two copies - one at the head and other at the original position) and recursively call the function on the rest-of-the-list. Let’s go for it:

let rec ssort lst =
  match lst with
  | [] -> []
  | _ -> let m = find_min lst in
         m::(ssort (rem m lst));;

That’s all folks! Have a great week ahead!

Let’s put on our thinking-in-recursion hat and put to use all that we have learned from our examples. We will do this by working out only two (so this will be a short post) examples that will use the recursion concepts that are bread and butter for us now.

As a first example, we will write a function to eliminate consecutive repetitions of elements in a list. For example, if we pass the list [1;1;2;2;3;3;3;4;5;5] to our function, it should return [1;2;3;4;5], after removing the repetitions. How do we go about doing this? The moment we see consecutive repetitions, we know that we can easily track this by observing any two consecutive elements in the list while traversing the list. We need to observe at least two consecutive elements in order to find out if they are repetitions. So far, in our previous examples, we have usually been observing one element, the first element of a list (or a sub-list) calling it the head and denoting it h. Remember the pattern-matchings of the form | h::t -> in our previous code snippets? We were observing an element h concatenated with a list t. Now, we need to observe two consecutive elements instead of one, to check if they are repetitions - something of this shape | h1 :: h2::t. Now, we can compare h1 and h2 and check if h2 is a repetition of h1. If they are not the same, we can always treat h2::t as the rest-of-the-list, which we called t (as in h::t) in our previous examples. Now, let’s jump in to the algorithm:

1. Base case - if it’s an empty list, nothing to check so we will just return an empty list
2. Otherwise - we think of the list to be made up of a head element x1 and the rest-of-the-list. The rest-of-the-list part we will further expand (in order to allow for checking repetitions). So, let’s say the rest-of-the-list is made up of x2::x3 - x2 is the head element of rest-of-the-list and x3 is the rest-of-the-list part of our original rest-of-the-list. Our pattern to match would look something of this shape: x1 :: (x2::x3 as t) - the as t just gives a name t to x2::x3.
   • if x1 and x2 are the same, then we recursively call the function on x2::x3. But, we threw x1 away and that’s fine because it was meant to be eliminated. We still have x2 that has the same value.
   • If x1 and x2 are not the same, we know that x1 does not have a doppelganger following it, and so we will include it in our result list that we will eventually return. We just append x1 to the result of the function call on rest-of-the-list.
3. Any other pattern, we just return the same pattern. Why do we need this? Because we want the patterns we match to be exhaustive - to cover all the cases. Suppose we have a list with a single element, this pattern would match that.

let rec compress lst =
  match lst with
  | [] -> []
  | x1 :: (x2::x3 as t) ->
     if (x1 = x2) then compress t
     else x1 :: compress t
  | smth_else -> smth_else;;

It turned out to be pretty simple, right?

Now, let’s work out another example before our enthusiasm dies down. Let’s do insertion sort. We will write it out as two recursive functions. Wait, don’t run away. It’s going to be simple. First, let us write a function that inserts an element x to a list lst, and it will insert x in such a way that the element next to x in lst would be great than x and the element before it would be less than or equal to x. Why are we writing this function? This is not insertion sort. Wait, it will be clear in a minute. We will call this function insert, takes two arguments x and lst.

1. Base case - if lst is empty, we just insert x into the empty list and return it
2. Otherwise, we have to traverse the list and see where to insert x. If head element is greater than x, it is easy - we just insert x at the head of the input list lst and return it. If not, we look for a position in the rest-of-the-list t to insert our x.

let rec insert x lst =
  match lst with
  | [] -> [x]
  | h::t ->
     if (x <= h) then x::h::t
     else h::(insert x t);;

Now, we will use the above function to write our insertion sort function isort. Just think what would happen if lst was already sorted in the above case. In that case, we would be inserting x to lst to maintain sorted order (just because of the rules that we imposed for inserting x). Let’s write down the algorithm.

1. Base case - if lst is empty, return the empty list
2. If the list has just one element, it is trivially sorted, just return the input list
3. If the list has two or more elements, pick elements one by one, starting from the head element h and use our insert function to insert it into the appropriate position.

let rec isort lst =
  match lst with
  | [] -> []
  | [x] -> [x]
  | h::t -> insert h (isort t)

Let’s check if it works on a simple test example:

let l1 = [1;7;9;3;11;2;10];;
isort l1;;
(* - : int list = [1; 2; 3; 7; 9; 10; 11] *)

That’s too much for my head for today. Let’s do more interesting examples in future posts when we get into the concept of tail recursion.

Let’s take a small break from OCaml and recursion and learn some data analysis. For this purpose, I am using python and a couple of libraries like Pandas, Numpy and Matplotlib, which will help us in preprocessing the data, some numerical data-types as well as plotting the data, respectively. In future posts, we will see more such awesome libraries.

For this post, let’s just focus on a Pokemon dataset that I happened to come across in Kaggle. Although I have never played Pokemon and never knew the different Pokemon characters, this is a nice simple example to get us started.

You may want to install python - I personally like Anaconda because it offers a wonderful platform with code editor as well as a console for visualization, etc., which makes it easy to play around and learn. I installed Anaconda and use their development environment Spyder.

Let’s get started right away. First, we import the libraries we will use for this short tutorial.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

We will use these libraries only very minimally for this short post, but they are very powerful and we will see more of their features in future posts. If you create a (free) account in Kaggle, you can download the Pokemon dataset. I have downloaded it and saved it in a file named Pokemon.csv. We will use Pandas read_csv function to read the downloaded csv file.

pokemon_data = pd.read_csv('Pokemon.csv')

We will call it pokemon_data. Pandas refers to this type as a dataframe. If you look at the dataset the first column is just an index, so it’s useless for our analysis purposes. So we will go ahead and grab only the rest of the columns (and all the rows).

pokemon_data = pokemon_data.iloc[:, 1:13]

Here [:, 1:13] says that “grab all the rows (denoted by :) and columns 1 to 13. Now, let’s explore the data a bit. It’s always a good idea to take a quick look at the dataset to see what are the different columns and what kinds of values or informations they indicate about the dataset. In this case, I see that there’s a column called Generation and it seems to take values between 1 and 6. Probably there are six generations of Pokemons, at least to my understanding. Now, let’s try to see how many Pokemons are there in each generation. If it were a population dataset, this is analogous to finding out how many people are in each continent, or something like that. I will call the number of generations by the variable no_gens. We need to pick the column named Generation and count the number of unique entries. Since there are 800 Pokemons in all and they belong to one of the 6 generations, there will be multiple rows that contain the same value for Generation and hence we need to find the number of unique values (which after having a quick look at the dataset we know is 6, but it is always better to confirm algorithmically and store in a variable). We achieve this by the function unique() applying it on the column. We extract the specific column by using the column label, in this case Generation. Similarly we count the number of values in each generation using the function value_counts()

no_gens = pokemon_data['Generation'].unique()
count_per_gen = pokemon_data['Generation'].value_counts()

Let’s try to plot the above values to have a better visual representation. I will use matplotlib’s pyplot library utilities for this purpose. It is very simple and intuitive to use. We will plot a bar chart - so we need to find out the values for x and y axes. Let’s first label the plot and the axes.

plt.xlabel('Generations')
plt.ylabel('Number of Pokemons')
plt.title('Number of Pokemons of each generation')
plt.bar(no_gens, count_per_gen)

This would result in a plot as shown below:

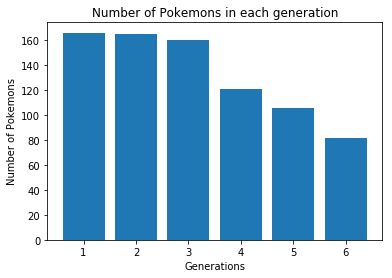
That was pretty quick. Let me stop here and let you all digest the information presented. We will analyze the Pokemon dataset more in the coming posts.

Let’s continue from our earlier post and practice some more simple problems just to get more and more familiar with recursion.

Let’s start by writing a simple function to find the last element of a given list lst:

let rec last_elem lst =
  match lst with
  | [] -> None
  | [x] -> Some x
  | h::t -> last_elem t;;
(* val last_elem : 'a list -> 'a option = <fun> *)

This is also a nice way to introduce Some and None in OCaml. Just like how we have 'a list which can be an int list or a string list or char list, OCaml also has this wonderful 'a option type that can be nothing (None) or some type (Some). Note however that 'a option type is not the same as 'a. So, if the type is 'a you can ask the compiler to treat it as an int, for example. But you can’t do the same with 'a option type. For friends of Java, C programming languages, you can think of None as similar to null type.

type 'a option = Some of 'a | None

For those JavaScript fans wondering if they can use similar Some and None in JavaScript, I found an option type implementation here that provides this. I should admit that I have never used this implementation but it seems to serve the same purpose for JavaScript.

Let’s test our last_elem function on an example.

let l1 = [1;2;3;4];;
last_elem l1;;
(* - : int option = Some 4 *)

Let’s move on and practice some more examples. Let’s now try and grab the last and the last-but-one elements from a list.

let rec last_two lst =
  match lst with
  | [] | [_] -> None
  | [x; y] -> Some (x, y)
  | _::t -> last_two t;;
(* val last_two : 'a list -> ('a * 'a) option = <fun> *)

('a * 'a) indicates a tuple - a pair in this case. For example, (3, 4) would be of type (int * int). Let’s check our implementation:

last_two l1;;
(* - : (int * int) option = Some (3, 4) *)

Let’s now make it more generic and write a function to find the k^th element of a list and let’s give our function a very creative name kth.

let rec kth lst k =
  match lst with
  | [] -> None
  | h::t ->
     if (k=1) then (Some h)
     else kth t (k-1);;
(* val kth : 'a list -> int -> 'a option = <fun> *)

Let’s check our implementation on l1 again:

kth l1 2;;
(* - : int option = Some 2 *)
kth l1 6;;
(* - : int option = None *)

When we try to find the 6^th element of the list l1, we get None type as a result as the list contains only 4 elements.

Let’s now try to reverse an input list. Relax! It just sounds complicated. It is actually super simple when you think in terms of recursion.

let rec lst_rev lst =
  match lst with
  | [] -> []
  | h::t ->
     (lst_rev t) @ [h];;
(* val lst_rev : 'a list -> 'a list = <fun> *)

Recall from our previous post that @ is the OCaml operator for list concatenation. It is a straight forward observation that after the first recursive call to rev_lst, the head element h is pushed to the last and in each recursive call the first element would keep getting pushed to the end of the result list.

lst_rev l1;;
(* - : int list = [4; 3; 2; 1] *)

This post is getting long. Please don’t stop reading it! I promise, just one more example to finish this post! Let’s write a function to remove an element from k^th position in a given list:

let rec rem_kth k lst =
  match lst with
  | [] -> []
  | h::t ->
     if (k = 1) then t
     else h::(rem_kth (k-1) t);;
(* val rem_kth : int -> 'a list -> 'a list = <fun> *)

rem_kth 1 l1;;
(* - : int list = [2; 3; 4] *)
rem_kth 6 l1;;
(* - : int list = [1; 2; 3; 4] *)

That’s all folks. If you have reached this line of this post (assuming you didn’t start reading from the last line), Congratulations for sticking around!

A break from recursions and algorithms for today! But still sticking to the broader goal of education and learning. I am a big fan of radio programs and in particular NPR. Over the weekend, I happened to listen to a very interesting program on education. Hosted by Guy Raz, last week’s episode of TED Radio Hour focussed on education and learning - specifically how it is changing with technology. It was a very interesting podcast and I really encourage all of you to make some time to listen to it. Below is a link to the podcast.

It is an added motivation for me to use more avenues to share my knowledge with the many in this world, as much as I learn through the many channels and from the many wonderful people on this planet.