Let us look at some fundamental data structures which are just a collection of primitive data types. For example, an array of integers is a collection of integers, a string is a collection of characters, etc.

Here, we are interested in Linked Lists which are just a collection (list) made by linking together some data-types (node). The data-types themselves could be any primitive or a data-type formed of primitive types. For simplicity, we will discuss linked lists of integer nodes. The building block of the linked list is a node and nodes are chained (linked) together using pointers, just a data-type that stores the address of the next node. The following sketch would explain it better.

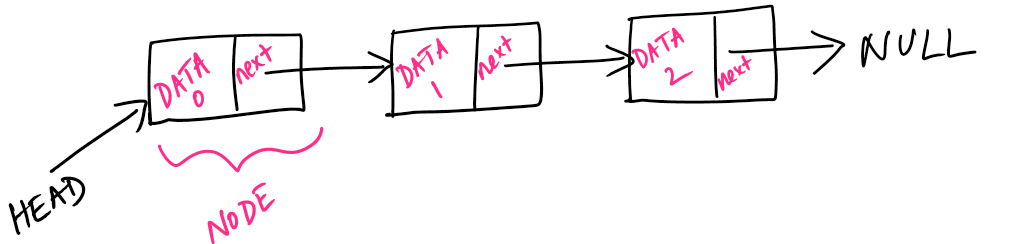
Here is how you would describe a node and a linked list as C++ classes:

class Node {
  public:
    int data;
    Node *next;
  public: 
    Node (int item);
};

We denote the fist node of the list as “head” node which will come handy when we have operations that traverse the list. The next pointer just stores the address of the next node, as shown in the image below.

class LinkedList {
  private:
    Node *head;
    int length;
  // constructors and member functions
  ...

Today, let us see how to compute the greatest common divisor (GCD) of two given input numbers. Although it is a very easy problem with a relatively straight-forward implementation, the beauty of the problem is that the algorithm was discovered more than 2000 years ago by a Greek mathematician Euclid, after whom the algorithm is named.

It uses the concept of modular arithmetic as discussed in the previous post. Put simply, the gcd of two given integers x and y is just the greatest number that divides both x and y. For example, the greatest common divisor of both 6 and 9 is 3. The obvious approach to compute the gcd if two given numbers is to factor both the numbers, pick out the common factors and multiply them. For example, 6 = 1 x 2 x 3 and 9 = 1 x 3 x 3, and the common factors being 1 and 3. Euclid’s algorithm uses the following formula:

If x >= y, gcd(x, y) = gcd(x mod y, y). As you see, the recursion is built in the description itself. Here’s an implementation:

int euclid_gcd (int x, int y) {
  // base case
  if (y == 0)
    return x;
  else
    return euclid_gcd(y, x % y);
}

One has to note that in the recursive call, the first argument became y and the second x mod y. This is because of the following lemma:

If x >= y, then x mod y < x/2.

So, the arguments x and y decrease with each recursive call. The applications of modular arithmetic is very wide, some of which we will see in future posts.

Let us chat about Modular Arithmetic - let’s start with a fun question that I actually happened to read in one of my textbooks on Algorithms.

Suppose you binge watch an entire season of some television show in one sitting, starting at midnight and suppose there are 25 episodes of the show, each lasting 3 hours. At what time of the day will you be done?

So, you start at midnight and watch for 25 x 3 = 75 hours non-stop. Since our clocks reset every 24 hours (Othewise, we would need several million digits to say the time!), we divide 75 into chunks of 24 hours, which is to say we compute modulo 24 and 75 mod 24 = 3 and so we will finish at 3 am. The way to think about modular arithmetic is to think of something that restricts numbers to a predefined range {0, 1, ..., N-1}.

Modular arithmetic has some beautiful properties that are very useful in several application domains, especially cryptography. We will get to learn about them in future posts.

In a previous post we saw how to write a recursive function to compute permutations of characters of a string. But we were computing redundant permutations when the input string had duplicated characters, as in the input string “AAB”. What could we do to avoid the redundant computations?

Intuitively we need to avoid some recursive calls that we know will lead to redundant computations. The sub-trees corresponding to this redundant computation are marked red in the sketch below:

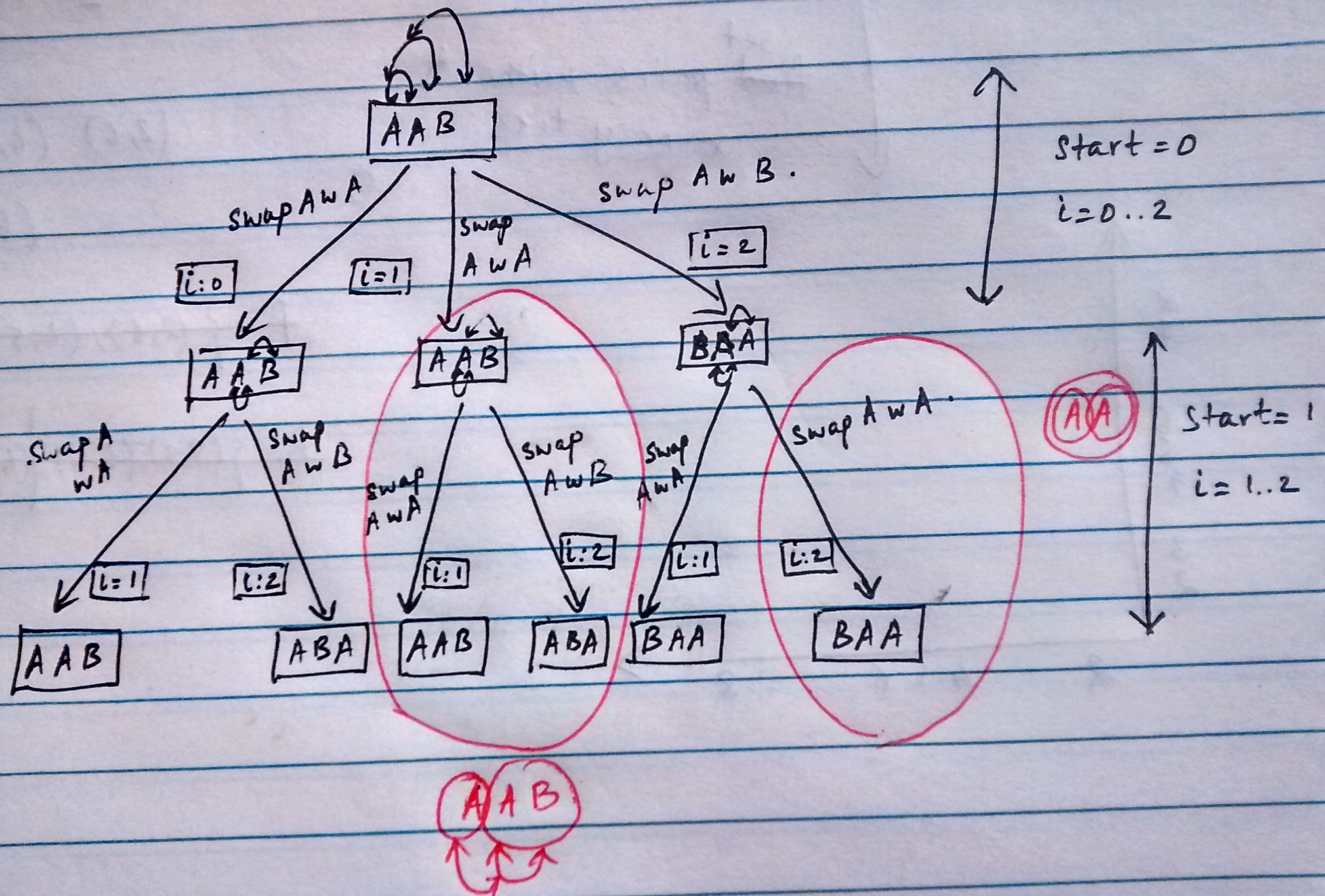
What it indicates is that when we have the substring that we are processing (by walking through the characters in the substring) we look at the characters we process and decide if we want to go down that recursive path.

Let’s go through a couple of paths in the recursion tree above and try to figure this out:

1. (start:0, i:0): The string we are staring with is AAB, substring starting at start is AAB and substring starting at i is also AAB (as i is start to begin with). Now we swap s[start] and s[i] which are both A. Now we call the _permute() with start incremented by 1. a. (start:1, i:1..2): Now the substring starting at start is AB (as start is 1) and substring starting at i is AB. Further s[start] is A and s[i] is also A. We hence perform a swap producing AAB and backtrack. Now, i:2 and so s[start] is A and s[i] is B. We swap A and B and get ABA.

2. (start:0, i:1): The string we are staring with is AAB, substring starting at start is AAB and substring starting at i is also AB (as i is 1 now). We have substring_from_start different from substring_from_i but s[start] is the same as s[i] which means that if we do a swap, we will yield the same thing and also we would have come across this earlier as we have processed the substring corresponding to this i. So we avoid going down this path and start working through start:0, i:2.

So the condition we are looking for traversing is that substring(start) and substring(i) are same and further the starting character at start and i are the same. Further, if substring(start) and substring(i) are different and the starting characters are different, we go ahead with the traversal (as in start:0, i:2).

Here is the modified permute() function with the condition incorporated:

void permute(string s, int start, int end) {
  int i;
  if (start == end)
    cout << s << endl;
  else {
    for (i=start; i<=end; i++) {
      // handle duplicates
      if ((s.at(start) != s.at(i)) || 
          ((s.substr(start, end-start+1) == s.substr(start, end-i+1)) && 
           (s.at(start) == s.at(i)))) {
        swap(s[start], s[i]);
        permute(s, start+1, end);
        swap(s[start], s[i]);
        }
    }
  }
}

Hope you can refer to the sketch above, work through the example and feel convinced.

In one of the previous posts we saw how to compute all permutations of a list recursively. Let us attempt the same, but this time with C++, in what is called divide and conquer approach - essentially divide the input into smaller chunks and recursively call the function on each of the smaller chunk.

Let us compute the permutations of say characters in a string. A string of n characters would have n! permutations. For example, if we have the string “ABC”, the permutations (6 in all) are:

ABC
ACB
BAC
BCA
CBA
CAB

We shall do it by going through the string of characters and iteratively swapping each character with the neighbouring character to get the permutation. For example, for the string “ABC”:

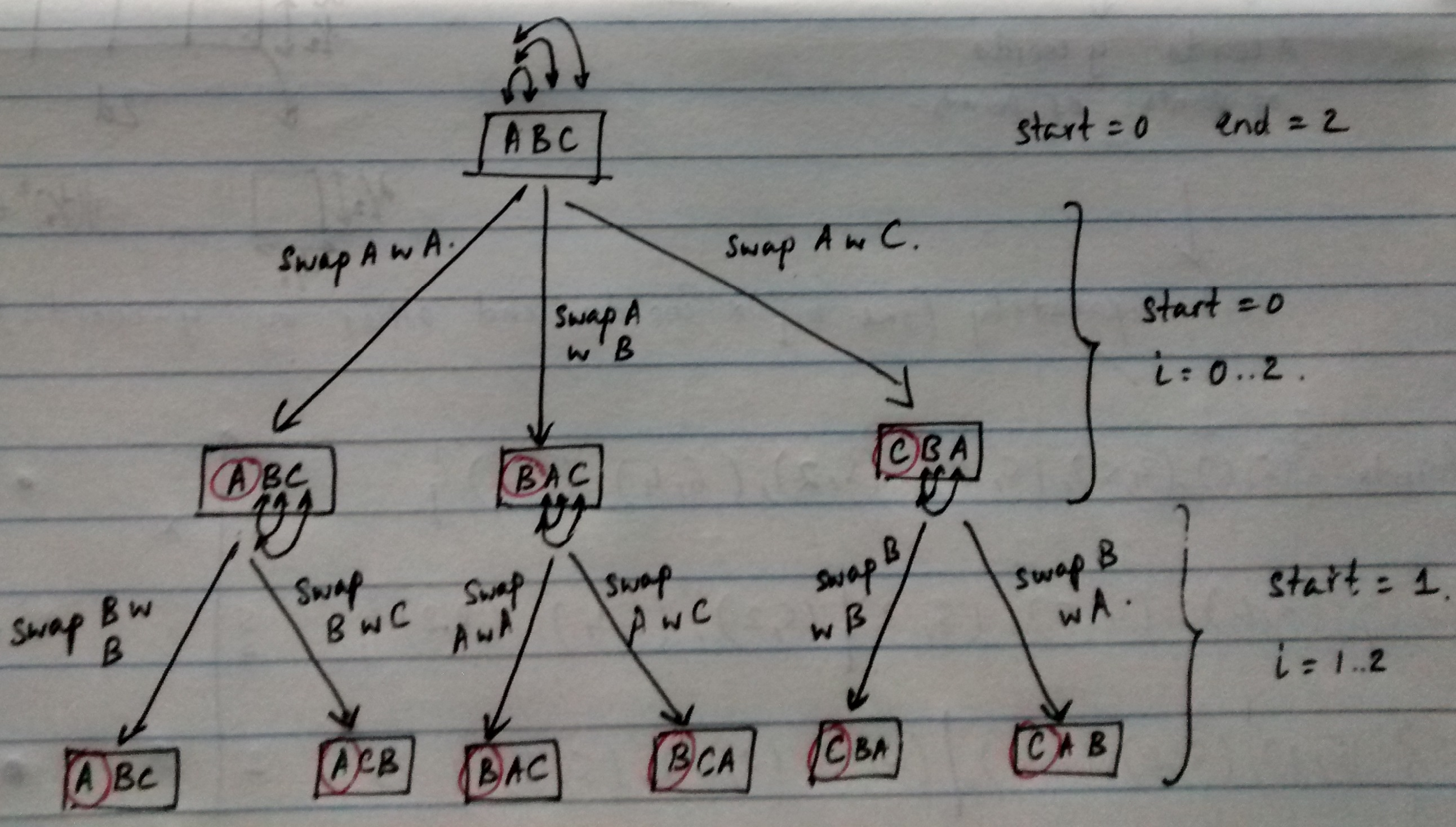
Here is a function permute() implementing the traversal: We are given a string s with starting index start and ending index end.

void permute(string s, int start, int end) {
  int i;
  if (start == end)
    cout << s << endl;
  else {
    for (i=start; i<=end; i++) {
      swap(s[start], s[i]);
      permute(s, start+1, end);
      swap(s[start], s[i]);
    }
  }
}

What happens if we use the above algorithms to find permutations of strings that have duplicated characters? For example, the string “AAB” would produce:

AAB
ABA
AAB  (*)
ABA  (*)
BAA
BAA  (*)

As you can see, we are computing the same permutation more than once (marked with *). How can we modify the above function to handle duplicates?