In our previous post we saw how to traverse and print the elements of a linked list in an iterative fashion. In this post, we will do the same (printing the elements of a linked list) but will do it in a fancy recursive way. This should remind you of our earlier posts on recursion, just that now we are in C++ world.

As we saw when we taught ourselves recursion using a more intuitive programming paradigm (functional programming using OCaml programming language), in any recursive function, we need to take care of:

1. Base case
2. Recursive step

In this example, the base case is just an empty list (NULL) and the recursive step is to just print the item as long as the list doesn’t fall into the base case.

void LinkedList::print_list_r () {
  Node *it = this->head;
  if (it == NULL) {            // base case
    cout << "NULL";
    return;
  }
  this->head = it->next;       // move forward
  this->print_list_r();        // recursive call
  cout << " <- " << it->data;  // print 
}

It is very important to understand this and our previous post as we will use the same idea to perform a more fancy operation on our linked list - to reverse it!

Now, that we are slowly becoming experts in navigating through the nodes in the linked list, let us see how we can print the nodes of our linked list. Again, the idea is very simple:

1. Start from the head node
2. Traverse the linked list until the list ends (node pointing to NULL)
3. On the way, print the data part (interesting part) of our list

void LinkedList::print_list () {
  Node *it = this->head;          // get the head
  while (it != NULL) {            // traverse till the end
    cout << it->data << " -> ";   // print node data
    it = it->next;                // move forward
  }
  cout << "NULL\n";
}

This is an iterative solution. We will soon look at a recursive solution to this. Stay tuned.

Now, let us progress with looking at slightly more complicated operations. In our previous post, we saw find operation that required us to traverse the list, but we needed to keep track of only one element while traversing - just match the element with the item we are trying to find and see if we found. But in some cases, we may have to keep track of more than one element - this is because we need to rearrange the pointers. Suppose, we have the following linked list with 4 elements:

19  ->  49  ->  21  ->  17  ->  NULL
(0)     (1)     (2)     (3)

and we are asked to delete the element at index 2 (its data being 21). We not only need to keep track of the current element to be deleted, we need to remember the previous element (in this case the one at index 1 with value 49) because this would point to 17 after deleting the one at index 2. Specifically, after the deletion, the linked list would look like this:

19  ->  49  ->  17  ->  NULL
(0)     (1)     (2)

In order to do this algorithmically, we keep track of two nodes, the current one (iterator denoted it in code below) and the previous node (denoted prev in code fragment below). As we traverse the list looking for the item at index, we decrement the index and once we find it, we rearrange the pointers - in particular, we set delete the node and attach prev to the rest of the linked list that followed the deleted node (i.e., the list pointed to by the deleted node’s next). Besides, we also need to handle cases when the index is ‘0’, i.e. we are trying to delete the first node or if the given index does not exist at all. A visual sketch is given below, followed by the method to perform the deletion.

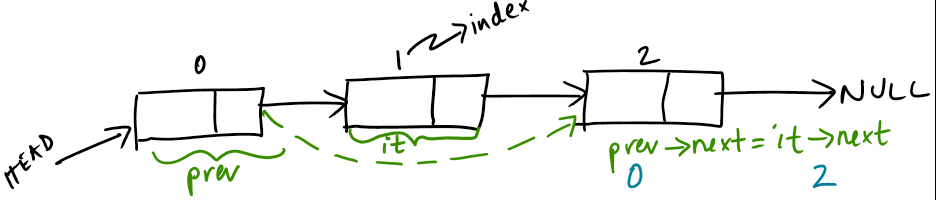
void LinkedList::delete_at_index (int index) {
  if (index >= this->length || index < 0)
    throw out_of_range("Index out of range for the linkedlist");
  Node *it = this->head;
  Node *prev = NULL;
  while (it != NULL) {
    cout << ":: index: " << index << ":";
    if (index == 0)
      break;
    index--;
    prev = it;
    it = it->next;
    cout << " (prev->data, it->data) : " << prev->data << ", " << it->data << endl;
  }
  if (prev == NULL) {
    this->head = it->next;
    delete it;
  }
  else {
    prev->next = it->next;
    delete it;
  }
}

In this post, let us see how to find if a given item exists in the linked list. Conceptually, it is very simple - just go through the nodes one by one and see if the data matches the item given as input. But, where do we start the traversal from? This is what we use the head pointer for. And when do we stop? Obviously, if we find the item we are looking for, we stop. We might also not find the item at all, in which case we traverse all of the list until we hit the NULL node (that indicates the end of the list).

Node *LinkedList::find (int item) {
  Node *it = this->head;
  while (it != NULL) {
    it = it->next;
    if (it->data == item) {
      return it;
    }
  }
  return it;
}

Having introduced linked lists in our previous post, let us look at some operations on such a data structure. Specifically, let us look at how to insert a new item (a new node) to a linked list. Typically, we start with an empty linked list (denoted by just one node, the NULL node) and grow it by adding more and more items. The usual approach to adding a new item is to form a node (the building block) for the new item and then attach the item to a position in the linked list - by default we choose to add it to the head.

Node *LinkedList::insert_item (int item) {
  Node *new_node = new Node(item); // form the building block
  new_node->next = this->head;     // set the next pointer
  this->head = new_node;           // make new node the head
  this->length++;                  // update the length
}