In a previous post you as a Marketing Manager was struggling to count the number of Cokes dispensed in order to compute the reward for the vendors. You made an expensive hire and made some progress, but wasn’t enough. Now, you are talking to your old academic friend over coffee and he is surpised why this is a big problem. He just exclaims that you should have used a Fenwick Tree instead.

So, what is this Fenwick Tree? It is an awesome data structure that allows you to compute the sum across a range of numbers without iterating over every element in the range. Of course, the earlier solution was able to do that as well. But the beauty that Fenwick Tree adds is that you could also do point updates in O(log n) time. And you don’t need nodes and pointers - the Tree structure is captured in the array itself. It was discovered by Prof. Peter Fenwick in 1994 in an article titled A new data structure for cumulative frequency tables.

How do we go about constructing one? We create an array of size one larger than the original input array (1 larger as we want to ignore the element at index 0 - we will soon see why) and copy over the elements of the input array in this new array starting from index 1. The interpretation of the tree (though the elements are stored in a linear data structure like an array) is that the indices which have LSB 1 (i.e. all odd indices) are interpreted as leaves of the tree. One level up are the elements that have the second bit set, and so on. Given an element, how do we find the parent node for it? We know that if the index corresponding to an element x has left-most bit set at position i then it’s parent should have the next bit set. For example element at index one (bit-0 set - 0001), and it’s parent is the one at index two (bit-1 set - 0010). Similarly element at index three (bit-1 set - 0011) has it’s parent at index four (bit-2 set - 0100). And element at index seven (bit-2 set - 0111) has it’s parent at index eight (bit-3 set - 1000). Given i, i + (i & -i) would give the parent’s index.

Let’s use this to construct our Fenwick tree. _arr is the given input array and the function returns the constructed Fenwick tree (array).

std::vector<int> FenwickTree::build_fwtree(std::vector<int> _arr)
{
  int n = _arr.size();
  std::vector<int> res(n+1);
  res.assign(n+1, 0);
  for (int i = 1; i <= n; i++)
    res[i] = _arr[i-1];
  for (int i = 1; i <= n; i++)
  {
    int p = i + (i & -i);
    if (p < res.size())
    {
      res[p] += res[i];
    }
  }
  return res;
}

We will see how to perform the other query operations in a future post. Stay tuned.

Suppose we have an array that is getting populated with some sensor from coke vending machines across a chain of restaurants - for every coke dispensed the element at the index of an array (you can imagine the indices correspond to the vending machine numbers) gets incremented by 1. And you being Coke’s regional marketing manager are tasked with identifying how many cokes were dispensed by say, machines 0 to 10 or some range i to j, in order to give rewards to those machine owners who sold more cokes.

How would you go about doing it? Of course, since you have the array, you could traverse the array from index i to j and sum up the elements. But this is an O(n) computation and you want to do it faster. You hire a Stanford graduate as a software engineer and he says we could create a second array that stores the cumulative sums so that the look up would be a constant time operation. You are excited! You give him a large bonus.

How to implement this simple solution? In C++, let us assume that we have setup the constructor and we will populate an auxiliary array (cfreq) that will hold the cumulative sum of elements of the input array _arr (that has numbers representing number of coke cans dispensed).

CumFreq::CumFreq(std::vector<int> _arr)
{
  int n = _arr.size();
  cfreq.assign(n, 0);
  cfreq = build_cfreq(_arr);

And the helper method build_cfreq() is just

std::vector<int> CumFreq::build_cfreq(std::vector<int> _arr)
{
  int n = _arr.size();
  cfreq[0] = _arr[0];
  for (int i = 1; i < n; i++)
    cfreq[i] = cfreq[i-1] + _arr[i];
  return cfreq;
}

Now that our cfreq contains the cumulative sums of original array elements, we can lookup this array in constant time to find out the cumulative sum of array ending at j (which is the sum of elements from 0 to j) or even sum of elements between indices i and j.

int CumFreq::rsq(int end)
{
  return cfreq[end-1];
}

int CumFreq::rsq(int begin, int end)
{
  return (cfreq[end-1] - cfreq[begin-1]);
}

But one of the vending machines numbered 0 had some wiring problem with its sensor and count of the number of cokes dispensed remained stuck at 0 for this machine. Now, the issue is fixed and shows the accumulated reading that the machine owner wants to update. He updates the values and that updates the original array _arr at index 0. Now, one has to recompute the array that holds cumulative frequency all over again. Can one come up with a better algorithm to avoid this scenario?

In our previous post we introduced the Stack data structure implemented using arrays. Now, we will see how to implement the operations on such a Stack - in particular we will learn how to implement the following methods:

• Push(item) - to push the input item into the stack
• Pop() - to pop an item from the stack
• top_of_stack() - to track the item in the top of the stack
• is_empty() - to check if the stack is empty

As we have already seen Queues, we pretty much have an idea of how to go about doing this. While in the case of a queue, we initialized front and rear and used those to see when we can add elements and which index to increment, here we initialized top (for top of stack) to -1 and we shall use that while performing our operations. We are tracking only top, so we increment the index when we push(), decrement it when we pop() and check the value to determine when the stack is empty as shown in the code fragment below:

bool Stack::push (int item) {
  // check if there's place to push
  if (top >= (MAXSIZE-1)) {
    cout << "Stack overflow!";
    return false;
  }
  // if there's place store the item
  else {
    arr[++top] = item;
    return true;
  }
}

int Stack::pop () {
  // check if there's anything to pop
  // or if the stack is empty
  if (top < 0) {
    throw out_of_range("Stack underflow!");
  }
  else {
    return arr[top--];
  }
}

int Stack::top_of_stack () {
  return arr[top];
}

bool Stack::is_empty () {
  return (top == -1);
}

That was easy!

In this post, we introduce Stack - a data structure closely related to Queue. It differs however in the order of operations that we perform on the constituent elements. While queue provided a FIFO (First-In-First-Out) order of processing, stack provides us LIFO (Last-In-First-Out), just as you would pick the last element that you put on the stack before picking out the other elements - just like in the stack of books below, it is very likely you added the blue book on the top very recently (Last-In) and you would pick out this book (on the top of the stack - First-Out) before picking out, say, the green books.

Again, as with queues, we can use an array or a linked list to store our elements. Let use see how to define a Stack class using an array implementation.

#define MAXSIZE 100
class Stack {
  int top;           // top of the stack
  int arr[MAXSIZE];  // array that implements the stack
  
  public:
    Stack ();

    bool push (int item);
    int pop ();
    int top_of_stack ();
    bool is_empty ();
};

Stack::Stack () {
  top = -1;
}

We add elements to our stack using the push() method, remove elements from the stack (actually from the top of our stack) using pop() method, and we also keep track of the top of the stack because that’s where interesting actions happen.

We will see the different methods in the following posts. Stay tuned!.

In our previous post, we saw how to model a Queue data structure using Linked List as a container for elements. Now, we will see how to implement the methods enqueue() and dequeue().

This is very similar to inserting a new element to a linked list as we saw earlier. To insert a new item, we construct a node with that item and a next pointer, add it to the list and adjust the pointers.

void Queue::enqueue (int item) {
  // if the queue is empty
  // front and rear are the same, i.e the new item
  Node *new_item = new Node;
  new_item->data = item;
  new_item->next = NULL;
  if (rear == NULL) {
    front = rear = new_item;
    return;
  }
  // else add it to the rear end 
  // of the queue
  rear->next = new_item;
  rear = new_item;
}

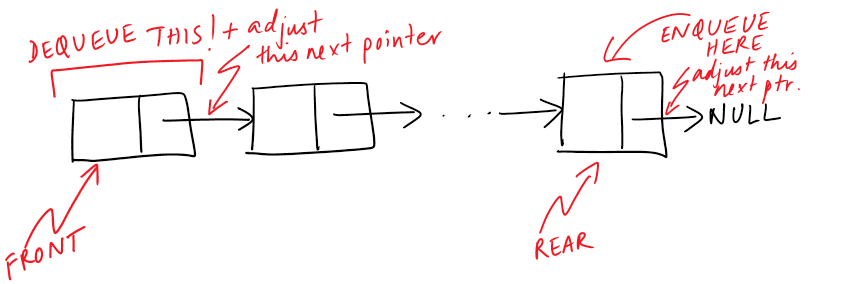
int Queue::dequeue () {
  int res;
  // check if the queue is empty
  if (front == NULL)
    throw out_of_range("Empty queue");
  
  // get the item to dequeue
  Node *dequeue_item = front;
  res = front->data;
  front = front->next;

  // now, if there was only one node
  // to pop front would point to NULL
  if (front == NULL)
    rear = NULL;

  delete (dequeue_item);
  return res;
}

bool Queue::is_empty () {
  return (front == NULL);
}

That’s all there is in Queues!