In a previous post we saw insertion and deletion of keys in a min heap. The heap property however is maintained by helper functions sink() and swim() which are used in deletion and insertion respectively. In this post, we will take a look at the implementation of these functions.

The main intuition behind the implementation is traversal of the tree from root towards the leaves (bubble down using sink()) and from leaf node towards the root (bubble up using swim()). The main objective is to maintain (or restore) the heap property which is just that the parent node is smaller than the children, which indicates that we need a way of identifying (and comparing) parent and children nodes. For any node k in the tree which is not a root, the parent node is at index k/2 and children nodes are at 2k and 2k + 1. So, all we need are to identify the elements at these indices, compare the values and keep swapping elements until heap property is restored. Besides we need to check boundary conditions (i.e. bubble up until we reach the root (k > 1)and bubble down (2k < n) until we reach the leaf).

void MinHeap::swim(int k)
{
  // parent of k : k/2
  while (k > 1 && (heap[k] < heap[k/2]))
  {
    std::swap(heap[k], heap[k/2]);
    k /= 2;
  }
}

void MinHeap::sink(int k)
{
  // children of k : 2k, 2k + 1
  while (2*k < n)
  {
    int j = 2*k;
    if (k < n && (heap[2*k] < heap[2*k+1]))
      j++;
    if (!(heap[k] > heap[j]))
      break;
    std::swap(heap[k], heap[j]);
    k = j;
  }
}

In a previous post we saw that constructing a heap (min heap) and retrieving min valued elements from it were very straight forward. Let us see how do we maintain the heap property (min heap property) of the data structure as we insert or delete items from it.

In order to achieve this, we will make use of two helper methods sink() and swim() which would be used in the client visible methods insert_item() and delete_item().

Let’s look at how to insert a given item into the heap. We insert it at the end (of the vector as we have implemented our heap using C++ std::vector) and we bubble up that element to it’s appropriate position. If this newly inserted element happens to be the min element so far, swim() would bubble it up all the way to the root. If not, it will occupy a position in the tree that satisfies the heap property - parent node’s key is smaller than that of childrens.

void MinHeap::insert_item(int item)
{
  heap[++n] = item;
  swim(n);
}

Similarly, while deleting the min element (which we know is at the root), we swap the current root element with the last element of the vector and delete the last element of the vector (point it to NULL). Now, the element occupying the root position may not be the min element anymore. So, we bubble down the root element using a call to sink() to an appropriate position in the tree that satisfies the heap property.

void MinHeap::delete_min()
{
  std::swap(heap[1], heap[n]);
  heap[n] = (int)NULL;
  n--;
  sink(1);
}

We will take a look at sink() and swim() methods in a future post.

In a previous post we came to know of this awesome data structure that could be used when we want to do fast retrieval of elements with maximum or minimum key values. In such cases, we do not need to sort the entire set of elements. In this post, we will see the implementation of Min Heap (which allows us to retrieve minimum element efficiently). Implementation of Max Heap follows a similar structure and is straight forward.

In this particular C++ implementation we use std::vector as the container for the elements of the heap. We ignore index 0 and our elements are stored from index 1. This is just to keep track of parent and children nodes easily. For any node k, the parent node would be at k/2 and children nodes at indices 2k and 2k + 1.

Further, we will start with the following signature that provides the client methods to insert a new key insert_item(), retrieve the min valued key get_min() and also delete the min valued key delete_min() from the structure.

class MinHeap
{
  private:
    std::vector<int> heap;
    int n;
  public:
    MinHeap(int capacity);
    int get_min();
    void insert_item(int item);
    void delete_min();
};

The constructor is straight-forward. We just create a vector of capacity one more than the specified one (as we are ignoring entry at index 0).

MinHeap::MinHeap(int capacity)
{
  heap = std::vector<int>(capacity + 1);
  n = 0;
}

Retrieving the min valued key is also straight-forward - just get the root of the tree. That is the beauty of this data structure. The way we accomplish having the min valued key always at the root is a little involved and it is incorporated into insert_item() and delete_min() methods.

int MinHeap::get_min()
{
  return heap[1];
}

We will see insert_item() and delete_min() methods in a future post.

If you are an Operating System (OS) and from the pool of tasks with attached priorities waiting to be executed, how would you pick the one that needs to be executed next? Sure, you could have them in an array, sort them (O(n logn)) and pick the highest priority one from the sorted data structure. Note that you don’t care about the task with the second highest priority at the moment (if you can execute only one task at a time). You only need to pick the highest priority task, which intuitively tells us that we do not need all the tasks sorted, but just a way to pick the one with the highest priority and that the ordering of the remaining tasks is not important.

Now suppose you are generating tasks to be sent to the operating system. You need to keep inserting new tasks with attached priorities to the pool of tasks. If you want to add a new high-priority task to the pool, you would like to put it in such a position that would make it quick for the OS to query and fetch it. Again, you should not have to go through the priorities of all of the tasks in the pool in order to decide the position of the new task.

What data structure would fit the above task? You do not even have to be an OS, you could be a system allowing passengers (high-priority ones have first-class boarding passes, for example) to board an aircraft. That brings us to Priority Queue data structure that has heap property - i.e. it is a tree where the key with the highest (Max Heap) or lowest value (Min Heap) is at the root and the children nodes’ keys are smaller (or larger in the case of Min Heap) than the root’s key. So, every fetch operation can just get the key at the root instead of traversing the entire tree (looking at all tasks in the pool). Let us see how to implement a heap in the next post.

In our previous post, we found a way to compute the position of the right-most set bit in a given number. A key ingredient of that algorithm was isolating the right-most set bit. For example, given 10, which is 1010 in binary, how do we “isolate the right-most set bit” - i.e. generate a bit-vector where only the bit in the position of the right-most set bit, in our input number, is set. For our input number 10, it would be a bit-vector where only the bit in position 2 is set - 0010. Given 1010, how do we generate 0010?

We mentioned about 2’s complement notation for negative numbers in a previous post. For example, the number 2 represented using 4 bits would be 0010 while -2 represented using 4 bits would be 1110, where the bit position corresponding to right-most set bit in in the positive equivalent (+2) is set, while all the bits to the left are flipped.

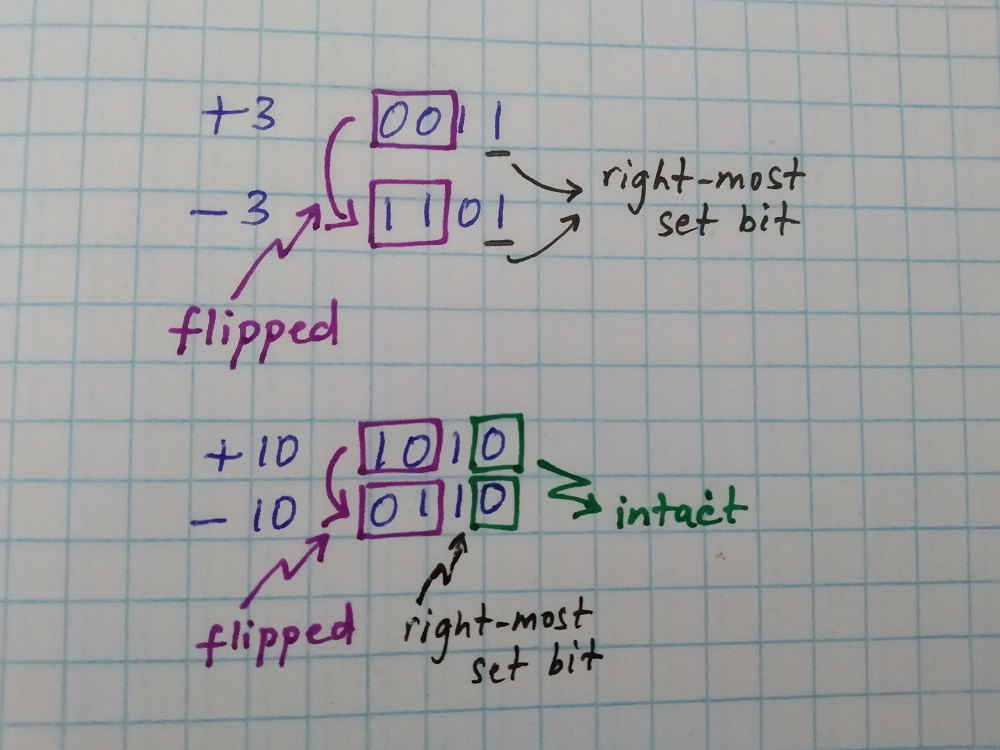
Now, if we & (bit-wise AND) our input number (x) with the negation of it (-x), we will be left with only one bit set, which corresponds to the position of the right-most set bit. So, the bit-wise operation we were looking for is & with the negation of the input number. Let us put all this together in a C algorithm (not that we already know the later part of the algorithm from the previous post):

int rightmost_set_bit (int x)
{
  // isolate the rightmost set bit
  x = x & (-x);
  int count = 0;
  while (x != 0)
  {
    x = x >> 1;
    count++;
  }
  return count;
}