In a previous post, we saw a recursive algorithm for computing the number of ways to reach atop n stairs. Let’s do a similar computation, this time for computing the number of ways you can combine coin denominations to arrive at a given amount. More precisely:

Given a set of coin denominations and a target amount, how many ways can you combine the denominations in such a way that the combination sums up to the target amount? You can assume that you have unlimited supply of denominations.

For example, if you have unlimited supply of $1 and $2 currency bills, how many ways can you combine them to return a change for $3? You could give three $1 bills, or a $1 bill along with a $2 bill (or alternately, a $2 bill along with a $1 bill, which is just a duplicate of the previous case just that I kept the $2 bill upon the $1 bill while giving).

Let us think recursively. Given a set S = {$1, $2} of bills, we could pick a $1 bill (to give) and now we have to think how many ways you can pick bills from our set S for the remaining amount of $2 ($3 the target amount - $1, the bill we already picked). Now, if you choose to pick another $1 bill, you have to think how many ways you can pick bills from our set S for the remaining amount of $1 ($3 the target amount - our first picked $1 - our second $1 pick). Now, we cannot pick $2 as we need only $1 and are just left with one choice - to pick another $1 from the set. This gives us one solution { $1, $1, $1 }.

Alternately, we could have first picked a $2 bill and then we would be left with no choice but to pick another $1, so that it adds up to $3. What we are essentially doing is picking a bill whose value is less than the target amount and then computing the number of ways you can pick bills for the remaining amount, i.e. target amount - picked bill amount (our recursive step). And if this difference becomes 0, then we have a solution that sums up to the target amount (our base case for recursion).

int coin_ways(std::vector<int>& S, int n, int target)
{
  // base case
  if (target < 0)
    return 0;
  if (target == 0)
    return 1;

  int ways = 0;
  for (int i = 0; i < n; i++)
  {
    ways += coin_ways(S, n, target - S[i]);
  }
  return ways;
}

If you try the above implementation on our example with S = { 1, 2 } and target = 3, you will get ways to be 3. And the three ways are { 1, 1, 1 }, { 1, 2 } and { 2, 1 }. What if we want only the unique ways? How would you go about modifying the above algorithm? That is we want to collapse { 1, 2 } and { 2, 1 } as just one count - after all it does not matter if I keep the $1 bill upon $2 bill or the other way around as long as I am returning bills that sum up to $3. Think about it.

Those who cannot remember the past are condemned to repeat it!

In our previous post we saw a recursive algorithm to compute the number of ways one can climb a fleet of n steps. If you draw the recursion tree for such an algorithm, we would soon find that we are computing some of the sub-problems repeatedly. We can do better by remembering (i.e. storing in some data structure) what we computed so that we can retrieve it and reuse it when needed again. Or in other fancy computer science parlance, we can use dynamic programming technique to solve such recursive problems more efficiently.

Here is the recursion tree for a hypothetical problem, similar to climbing stairs from our previous post where each function call for an input parameter value n leads to two calls for values n-1 and n-2. We can readily see, even in this very small example, that the all the function calls in the sub-tree rooted at 2 is computed again unnecessarily. One of the main ideas in dynamic programming is to store such computations so that we can reuse them when needed again.

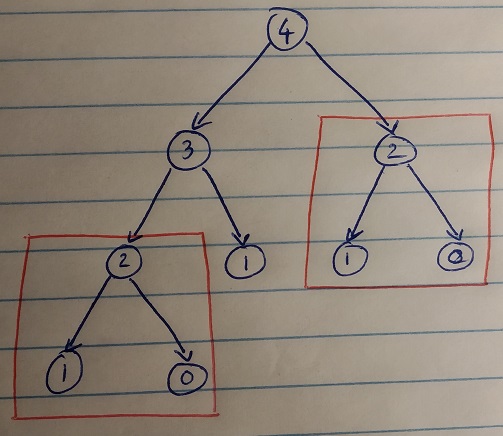
Let us try to use dynamic programming and rewrite our algorithm for computing the number of ways of climbing n steps. We shall use a simple array (a C++ vector) to store intermediate computations. More concretely, we will store the number of ways of climbing 1 step, the number of ways of climbing 2 steps, and so on. So, our array ways stores the number of ways - ways[i] gives us the number of ways of climbing i steps. As we saw in our previous post, the algorithm just needs to compute ways[i-1] + ways[i-2] for different values of i upto n and finally return ways[n] as the result.

int stairs(int n)
{
  std::vector<int> ways(n+1);

  // base case
  if (n <= 1)
    return 1;

  ways[0] = 1;
  ways[1] = 1;
  for (int i = 2; i <= n; i++)
    ways[i] = ways[i-1] + ways[i-2];

  return ways[n];
}

An astute reader would start thinking how this is different from divide-and-conquer approaches for solving recursive problems. I will let you think about it for now and find out for yourself what technique is beneficial for what specific structure of the recursive problem - that was already a hint there!

How many different ways can you reach atop a fleet of n step stairs taking one or two step jumps at a time?

This question might ring a bell for some who have heard about an Italian mathematician who computed a similar sequence for counting rabbits in his garden. Let us think about it using a smaller example and generalize the solution. Let us say we have only 2 steps to climb. Given the constraints (1 step or 2 step climbs only), we can complete 2 steps in the following ways:

1. 1 step, 1 step
2. 2 steps

2 possible ways. How about 3 steps?

1. 1 step, 1 step, 1 step
2. 1 step, 2 steps
3. 2 steps, 1 step

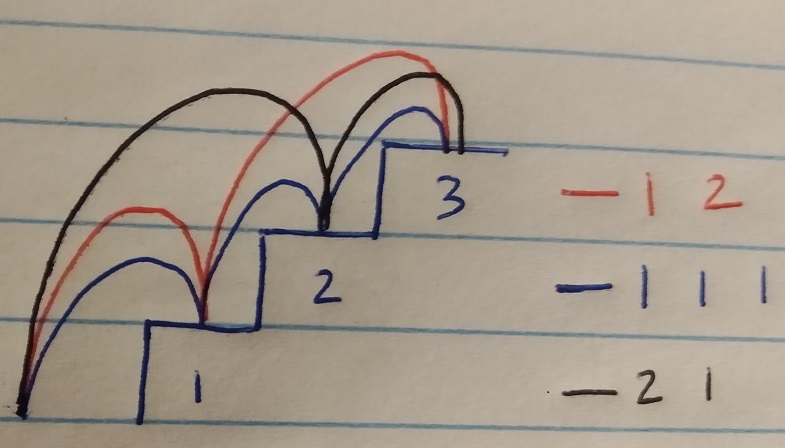
So, 3 possible ways. What about if we have an additional one to climb (i.e. total of 4 steps to climb)? We can do it in the following ways:

1. 1 step, 1 step, 1 step, 1 step
2. 1 step, 2 steps, 1 step
3. 1 step, 1 step, 2 steps
4. 2 steps, 1 step, 1 step
5. 2 steps, 2 steps

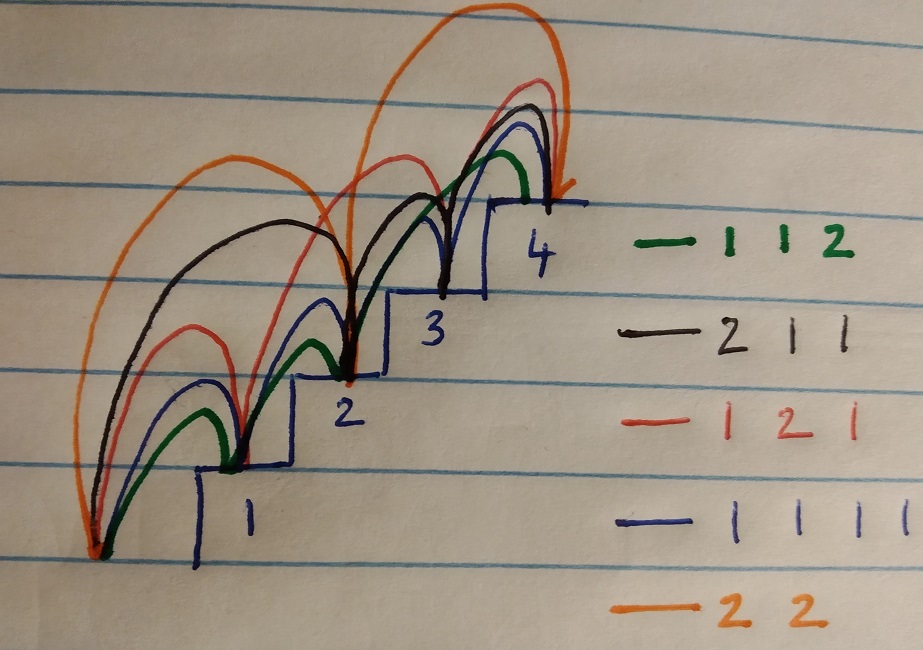
We also notice that the number of ways of climbing 4 steps is the number of ways of climbing 2 steps + the number of ways we could climb 3 steps. Recursively, we could compute for any n steps, given the constraints, we could climb it by computing the number of ways of climbing n-1 and n-2 steps.

int stairs(int n)
{
  // base cases
  if (n <= 2)
    return n;

  int res = stairs(n-1) + stairs(n-2);
  return res;
}

In our previous post, we saw a simple problem and a simpler solution to the problem. However, the cost was prohibitive (O(nd)). How can we reduce the time complexity? Let’s try to do it at the expense of some space.

The idea here is again very simple. Instead of doing 1 rotation d times, we would copy over d elements at ones and shift them together. Earlier needed only one temporary variable to store the first element of the array before moving it to the position of the last element. But now, we would need a variable that can hold d elements as we are going to move d elements at once. So our space complexity has gone up from O(1) to O(d).

void rot_arr_by_d(int arr[], int n, int d)
{
  // space: O(d)
  int* tmp = new int[d];
  // copy the first d elements from arr to tmp
  // time: O(d)
  for (int i=0; i < d; i++)
    tmp[i] = arr[i];
  // rotate the remaining n-d elements
  // time: ~ O(n)
  for (int i=0; i < n-d; i++)
    arr[i] = arr[d+i];
  // fill the remaining from tmp
  // time: O(d)
  for (int i=0; i < d; i++)
    arr[n-d+i] = tmp[i];
}

Since we had have d less than n as the problem statement, O(n) would dominate and this would be a O(n) solution. Can we do better than this?

Here is a very simple problem. Given an array of n elements and an integer d (less than n) how would you write a program to rotate (around) the elements of the array to the left by d elements? For example, if the input array (of size 7) is {1, 2, 3, 4, 5, 6, 7 } and d is 2, the output array would be { 3, 4, 5, 6, 7, 1, 2 }.

Let’s start simple. How would you rotate by 1? We would essentially move all the array elements to the left by one position, while moving the first element to the position of the last element. Essentially we would be moving n elements. Let’s write a function to do that:

void rot_arr_by_1(int arr[], int n)
{
  int tmp = arr[0];
  int i;
  for (i = 0; i < n-1; i++)
    arr[i] = arr[i+1];
  arr[i] = tmp;  
}

The time complexity of the above solution is O(n) while the space complexity is O(1) (one variable to store the initial element). Now, rotating by d is just rotating by 1 done d times.

void rot_arr_by_d(int arr[], int n, int d)
{
  for (int i = 0; i < d; i++)
    rot_arr_by_1(arr, n);
}

Now, the time complexity of the above function is O(nd). Can we do better than this?