In one of our previous posts we saw how Python’s memory management handles immutable variables in a program. Lists in Python are mutable. Let’s see how it works out.

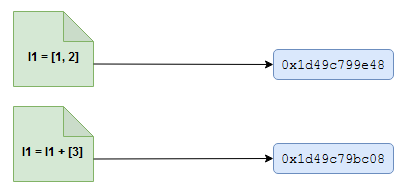
Let us consider a list l1 that contains [1, 2] and see what memory address it references.

def mem_addr(item):
    return hex(id(item))

l1 = [1, 2]
print (l1)
print ('memory referenced by l1: {0}'.format(mem_addr(l1)))

In my execution, it seems to reference the memory address 0x1d49c799e48. Now, let us concatenate a list containing a single element [3] to l1. Since lists are mutable, shouldn’t we expect the new list created out of concatenation to reference the same memory location? Let’s check it out.

l1 = l1 + [3]
print (l1)
print ('memory referenced by l1: {0}'.format(mem_addr(l1)))

We see that it references a new memory location (in my case 0x1d49c79bc08) different from the earlier one. What is happening? Aren’t lists mutable objects? Let us see in future posts when the memory manager would reference newly created lists to the same memory location as the initial list. Till then, play around with Python and discover more quirks.

Given an array of integers, how would you compute the subarray composed of consecutive array elements, that sums to 0? There are (n^2) such subarrays and traversing each of those in the worst case to compute the different sums would take (O(n)). But one could make it a little better by having a rolling sum computed as and when we are exploring the subarrays. Let us look at the naïve solution. Remember that we want subarrays formed by consecutive array elements.

We keep a marker (i) on each array element (outer loop), and search for the subarray starting from this marker to another one (j) while checking if the sum of array elements between i and j sum to 0.

bool zero_sum_subarray(std::vector<int> arr)
{
  int n = arr.size();
  for (int i = 0; i < n; i++)
  {
    int sum = 0;
    for (int j = i; j < n; j++)
    {
      sum += arr[j];
      if (sum == 0)
        return true;
    }
  }
  return false;
}

How can we make this algorithm better? Can we compute it in linear time?

In our previous post we saw how to compute all possible subsets of a set and we assumed there are no duplicates. Here, we will remove that restriction and see what modifications need to be done to our previous algorithm in order to accomodate the relaxation. The earlier algorithm referred to the input as a set, and I will continue referring to the earlier algorithm (although in strict mathematical terminology, a set does not have duplicates). So, the title of the post itself is misleading if you are a mathematics police.

First, let us understand what would be the output of our algorithm on an input set (or a list) that contains duplicates, say [1 2 2]. It is going to be:

[]
[1]
[1 2]
[1 2 2]
[1 2]
[2]
[2 2]
[2]

As you notice, there are duplicates in the result set as well [1 2], [2], etc. A careful observer must have already noticed that it requires just a one line change. Intuitively before we pick elements from our input set (containing duplicates) and insert them into our intermediate result set, we just need to check if we already encountered the element. If we sorted the input set à priori, the duplicates would be staying together and this would allow us to prevent inserting an element to our intermediate set a second time, if the previously inserted element was the same. In our traversal loop, we just need to check for this condition before we insert.

for (int i = start_index; i < input_size; i++)
{
if (i != start_index && (input_set[i] == input_set[i-1]))
  break;
...
...

Also, we sort the input set before we call the procedure:

std::sort(input_set.begin(), input_set.end());
all_subsets_rec(result, int_result, input_set, 0);

Try it out and convince yourself.

Let us try and compute all subsets of a given set of integers.

Let us try a recursive solution in this post. We will also see how to implement it in a more efficient manner in a later post. Suppose that the user is given the set of elements as a vector of integers and to further simplify, let us assume that there are no duplicates in the input set (and that’s why we call it a set). We want to return the set of all possible subsets that can be formed - a vector of vectors. At this point, we have some idea of what data-type we could use. If you are programming in C++, one could straight away use a std::vector. If you are using Python or some other functional language, you could use a list.

Let’s think recursively now. What would be the base condition? That is we are given an empty set as input. We just return. That was simple.

Now, if we had just one element in our input set, what would be our result? The result would have a set containing the one element, and an empty set (as empty set is a valid subset of any set). This already gives us an operational hint - may be, we can start with an empty result set to begin with and traverse the given input set and add elements from it to our result set. In this simple case, let us suppose that the input set is just [1]. Here’s how we would proceed

[]        - empty result set
[] [1]    - adding the one element from our input set

Let’s keep going. What happens when there are two elements in our input set? Say, [1 2]? As we saw above, we will start with an empty result set []. We can traverse the input set and pick and add more elements from it to our result set, until we exhaust the input set:

[]              - empty result set
[] [1]          - adding the first element
[] [1] [1 2]    - adding the second element

At this point, we have exhausted the input set. But we have not captured [2] as a part of our solution yet. What do we need to do in order to capture that? Just like how we added the first element 1 to our initial empty set, we should add only the second element 2 to our initial input set. In order words, we backtrack to the state (since we are going to be writing a recursive algorithm, this would correspond to popping from the recursion stack) where we had only the empty set, and add the second element. The entire sequence of operations would now appear like:

[]                - empty result set
[] [1]            - adding the first element
[] [1] [1 2]      - adding the second element
                  - ** backtrack **
[] [1] [1 2] [2]  - adding only the second element

We can keep going. Note that when we have three elements [1 2 3], we will need to backtrack to the state where our result had [1] and add 3 to it yielding [1 3] and later on (when? when we exhaust the rest of the input list) backtrack to the state where our result had [] and add 2, and similarly 3 to the empty result set. I would leave it as an exercise to work out the steps as we did above.

We see there are three major operations:

1. insert the intermediate result set to our result set of sets (like how we added empty set in the left most column above
2. traverse the input set starting from the index pointing to the first element, picking elements one by one and adding it to our intermediate result set, until we exhaust all the elements in our input set
3. backtrack (corresponding to moving the index to point to the second element) and pick and add elements one by one as in step 2.

Let’s write it in C++ language.

void all_subsets_rec(std::vector<std::vector<int>>& result,
                     std::vector<int>& int_result,
                     std::vector<int> input_set,
                     int start_index)
{
  int input_size = input_set.size();
  // base case
  if (input_size == 0)
    return;
  
  // populate result set of sets
  result.push_back(int_result);

  // traverse
  for (int i = start_index; i < input_size; i++)
  {
    // populate intermediate result
    int_result.push_back(input_set[i]);
    // recurse
    find_all_subsets(result, int_result, input_set, i+1);
    // backtrack
    int_result.pop_back();
  }
}

and the above recursive function is called in the driver program as:

std::vector<std::vector<int>> result;
std::vector<int> int_result;
all_subsets_rec(result, int_result, input_set, 0);

At the face of it, it looks like a very simple problem and it is. But this is one of those problems which is very easy to get it wrong. Many things could go wrong here - you could overflow some bounds, add the same element twice or more times to the result array and so on.

I recently started coding in Python as I was playing around with data science, statistics and machine learning libraries. As I started writing more and more Python (Python 3) code, I also started exploring how different it is from C/C++. Although I am very familiar with programming languages like OCaml, Python is giving me more surprising discoveries than in any other languages I have played with. Let us look at some of those together.

First is how Python’s memory management handles immutable and mutable data-types. For beginners, in Python everything is an object. Something declared like

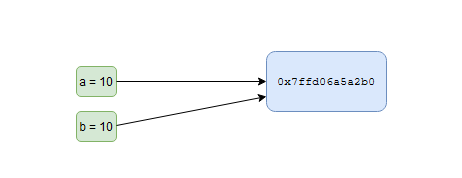
a = 10

results in an int object a that references a memory location. The memory location referenced by the object can be determined by using id() function and by convention you denote it in Hexadecimal number, so one often does hex(id(a)).

Now, let us see what is the memory referenced by our variable (actually a Python object) a.

print('memory referenced by a: {0}'.format(hex(id(a))))

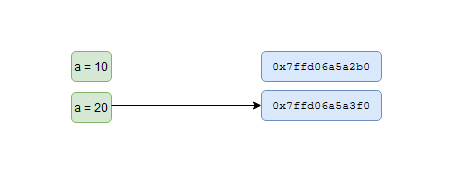
and it returns 0x7ffd06a5a2b0. Now, let us reassign a to value 20. Now, we see that memory referenced has changed to 0x7ffd06a5a3f0, instead of changing the value in the location referenced earlier.

a = 20
print('memory referenced by a: {0}'.format(hex(id(a))))

In programming languages like C or Java, the contents in the memory would be changed. However, in Python a new reference is created to a memory location containing the (updated) value 20. Now our previous int object is not referencing anything and Python’s garbage collector would reclaim it.