In a previous post we saw how to compute all the subarrays (formed by consecutive elements of an array) that sum to zero. Here, we are going to compute the maximum length one among all those subarrays. You might think why it needs a separate post - one can store all the computed subarrays in a vector and find the maximum of the sizes of the vectors. But one could in fact keep track of the maximum length as and when we compute the individual subarrays that sum to zero.

Let us look at the naïve approach, as it would be much simpler to understand, and incorporate this computation into it.

void max_len_subarr(std::vector<int> arr)
{
  int n = arr.size();
  int max_len = 0;
  for (int i = 0; i < n; i++)
  {
    int acc = 0;
    for (int j = i; j < n; j++)
    {
      acc += arr[j];
      if (acc == 0)
      {
        int len = j - i + 1;
        max_len = std::max(len, max_len);
      }
    }
  }
  std::cout << "max len: " << max_len;
}

We initialized a variable max_len to 0 and update it as and when we find the starting and ending indices of the subarray that sums to zero. We can extend the same idea to the linear scan algorithm, as below:

void max_len_subarr(std::vector<int> arr)
{
  int n = arr.size();
  std::unordered_multimap<int, int> lookup;

  lookup.insert(std::pair<int, int>(0, -1));
  int max_len = 0;
  int acc = 0;
  for (int i = 0; i < n; i++)
  {
    acc += arr[i];
    if (lookup.find(acc) != lookup.end())
    {
      auto it = lookup.find(acc);
      while (it != lookup.end() && it->first == acc)
      {
        int len = i - (it->second + 1);
        max_len = std::max(len + 1, max_len);
        it++;
      }
    }
    lookup.insert(std::pair<int, int>(acc, i));
  }
  std::cout << "max len: " << max_len << std::endl;
}

In an earlier post we saw how Python’s memory management behaves when dealing with immutable objects. In this post, let us see another immutable object, this time a tuple and examine how Python deals with it.

Let us consider a tuple of integer objects t = (1, 2, 3). We see that it references memory address 0x1dd65ac45e8

def mem_addr(item):
    return hex(id(item))

t = (1, 2)
print('memory referenced by t: {0}'.format(mem_addr(t)))

What happens if we try to mutate or update the tuple object above, t? We see that it creates a new reference to a new object (at 0x1dd65a514c8), instead of updating the earlier object. And the earlier reference would be reclaimed by the garbage collector.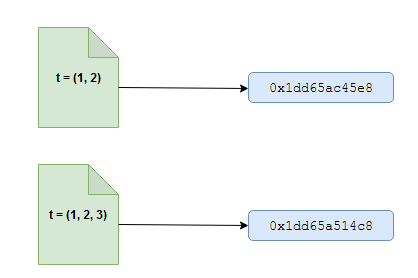

t = (1, 2, 3)
print('memory referenced by t: {0}'.format(mem_addr(t)))

This is because tuples are immutable objects, more like integer objects we saw in an earlier post.

So, all is clear and good, right? Wait until a future post on tuples again.

In our previous post we saw how to check if there is a subarray (formed of consecutive array elements) that sums to zero, in linear time. We were also thinking how to go about storing all the subarrays that sum to 0, as there could be more than one. Since we returned a Boolean result as soon as we found a subarray that sums to zero, we did not manage to find the second subarray that sums to 0, if such a subarray exists. Now, we will make an attempt to do that.

Intuitively, we know that we need to traverse the array as before and keep track of the accumulated sum of array elements as we traverse. We hash these values and do a lookup of it every time we encounter a new element (and hence an updated accumulator value) as we traverse.

     [initial subarray][0 sum subarray][some subarray][0 sum subarray][last subarray]
     <--------------- x ------------- y ------------ x'------------- y'------------->

At y we may find that the accumulator value already exists in our hash (as the subarray in the window between x and y sums to 0). On a lookup at y, we would get the index pointing to x and our current iterator (say i) would be at y. We can print out the values between x and i (or store it in some container), keep traversing the array until we encounter the ending index y' of the next subarray that sums to 0.

void all_zero_sum_subarr(std::vector<int> arr)
{
  int n = arr.size();
  std::unordered_multimap<int, int> lookup;
  lookup.insert(std::pair<int, int>(0, -1));
  int acc = 0;
  for (int i = 0; i < n; i++)
  {
    acc += arr[i];
    if (lookup.find(acc) != lookup.end())
    {
      auto it = lookup.find(acc);
      while (it != lookup.end() && it->first == acc)
      {
        std::cout << it->second + 1 << ".." << i << std::endl;
        it++;
      } 
    }
    else
      lookup.insert(std::pair<int, int>(acc, i));
  }
}

Can you see why we are using unordered_multimap instead of unordered_map here?

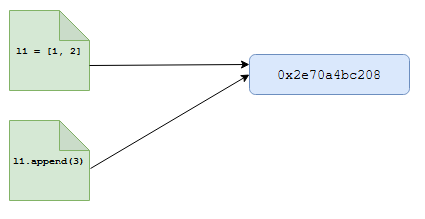
In an earlier post, we saw how lists, despite being mutable objects in Python are somewhat confusing when it comes to certain operations. Let us play some more and see how they behave when we concatenate lists using append().

l1 = [1, 2]
print (l1)
print ('memory referenced by l1: {0}'.format(mem_addr(l1)))

In my execution the memory referenced by l1 seems to be 0x2e70a4bc208. Now, as in our earlier example, let us append 3 to l1, but this time using the append() function.

l1.append(3)
print (l1)
print ('memory referenced by l1: {0}'.format(mem_addr(l1)))

Now, we see that the new list object (after appending 3) references the same memory 0x2e70a4bc208 as before. So, when it comes to append() Python’s memory manager seems to treat lists as a real mutable object. Python developers, especially new ones, need to be careful and understand these quirks thoroughly.

In a previous post, we computed a subarray composed of consecutive array elements that sums to 0 and were wondering if we can do it in linear time. And in fact, we can do it in linear time, by remembering the intermediate subarray sums rather than recomputing them.

We maintain a set to store the sum seen so far. Our array may be (if it has a subarray composed of consecutive array elements that sum to 0) composed of such blocks of elements:

     [initial part of the array][subarray that sums to 0][later part of the array]
     <------------------------ x ---------------------- y ----------------------->

bool zero_sum_subarray(std::vector<int> arr)
{
  int n = arr.size();
  std::unordered_set<int> lookup;
  lookup.insert(0);
  int acc = 0;

  for (int i = 0; i < n; i++)
  {
    acc += arr[i];
    if (lookup.find(acc) != lookup.end())
    {
      return true;
    }
    else
      lookup.insert(acc);
  }
  return false;
}

Now, we initialize our memory 0. When we reach the index x, our accumulator (acc) would contain the sum of elements upto index x. As an when we traverse the array and compute the intermediate sums in the accumulator, we also see if our memory has seen the accumulator value and if it has not seen we populate the memory with the accumulator value. Now, when we go from x to y since the elements in this window would sum to 0, the accumulator value at y would be the same as at x (since the elements between x and y summed to 0 and did not contribute anything to the accumulator). And we have this value already stored in the memory (which we will know if we lookup the memory) and hence can confidently say that we have found the 0 sum subarray.

There may be more than one subarray that sums to 0. How do we capture and retain all the subarrays that sum to zero? Suppose we want to pick the longest subarray that sums to zero, how do we go about it?