Suppose you own a few small boats and are making money shipping goods between UK and continental Europe. Your boats are small and they have limited capacity. You have your busy days once in a while but almost always you need to choose the products so that you can create maximum value. Your fee is not based on the weight of the products rather on the value of the products that you ship.

Brexit vote happened and all of a sudden you get requests for shipping products that you have never shipped before. You are not sure how to decide which products to ship. Given a bunch of products like fish, cheese, expensive wine, Louis Vuitton bags, etc. along with their weight and their value, you want to decide how many of each item to include in order to get maximum value. Remember that you have small boats which have limited carrying capacity.

Several years ago, you got a CS degree and you think it might come to use now. You decide to write a program in order to figure out maximum value that you could obtain. All good. You pick up your chromebook and start framing the problem. You have a list of items - their weights and values. You know the capacity of your boat (you do it for one boat at a time, as if one boat is in France, one is in UK and the third is in Amsterdam).

a list w: weights of items
a list v: corresponding value of the items
threshold: capacity of your boat

Now, you can include the item to be carried in your boat or exclude it and tell the merchant to wait for the next trip or find another shipping agency. For an item i, once you decide to include it, your value would increase by v[i] and you will have threshold - w[i] capacity left in your boat. If you decide to exclude item i, you will have no value from that item (as you are not transporting it) but you will have threshold capacity to fill. It should be an easy problem then:

for each of the items, you find the max value from the two choices you have: including an item i or excluding the item i

It is as simple as max(incl, excl) where incl and excl refer to the value you obtain by deciding to include the item i or exclude the item i. Once you include the item i, you would be left with one less item in your candidate set to pick the next one. Intuitively you can keep recursing until there are no more items left or until your threshold is reached. You go about writing a recursive algorithm to help you decide.

int knapsack(std::vector<int>& w, std::vector<int>& v, int n, int threshold)
{
  // base case
  if (threshold < 0)
    return INT8_MIN;

  if (n < 0 || threshold == 0)
    return 0;

  // include the current element in the solution
  int incl = v[n] + knapsack(w, v, n-1, threshold - w[n]);
  // exclude the current element
  int excl = knapsack(w, v, n-1, threshold);
  return std::max(incl, excl);
}

Is this the most efficient way of writing this though? Think about it.

In an earlier post, we saw tuples, which are immutable data-types in Python, but in the case of a tuple of lists, we were able to modify the contents of the list. Now, we will see dictionary objects in Python and see if they behave as expected. Recall that dictionaries are mutable objects in Python.

def mem_addr(item):
    return hex(id(item))

d1 = dict(k1 = 1, k2 = 'a')
print('memory referenced by d1: {0}'.format(mem_addr(d1)))

The memory referenced by d1 seems to be 0x28be6286ee8. Now, let us try to modify the contents of our dictionary. In particular, let us add a new key and a corresponding value.

d1['k3'] = 10.5
print('memory referenced by d1: {0}'.format(mem_addr(d1)))

The memory referenced by d1 still seems to be 0x28be6286ee8. So, dictionaries seem to be well behaved. I like them.

However, for people who are still stuck with an older version (Python <= 3.5) and moving to Python >= 3.6, there are some surprises with dictionaries. For example, let us try with Python 3.6 first:

d2 = { 'a': 1, 'b': 2, 'c': 3, 'd': 4, 'e': 5, 'f': 6, 'g': 7, 'h': 8, 'i': 9 }
print(d2)

prints out:

{'a': 1, 'b': 2, 'c': 3, 'd': 4, 'e': 5, 'f': 6, 'g': 7, 'h': 8, 'i': 9}

And if you notice, the keys are in order they were specified when d2 was created. With Python <= 3.5 however, this was the output (v2.7.13):

{'a': 1, 'c': 3, 'b': 2, 'e': 5, 'd': 4, 'g': 7, 'f': 6, 'i': 9, 'h': 8}

The reason for the above surprise is just that in Python 3.6 dictionaries got an order-preserving implementation and it became a standard since Python 3.7.

In a previous post we were wondering if we can compute the elements (from a given unsorted array of integers) that result in maximum product faster than O(n logn). It turns out we can do a linear scan of the array, keeping track of the largest two and the smallest two elements. One of these pairs would result in the maximum product.

void maxprod(std::vector<int> arr)
{
  int n = arr.size();
  int max1 = arr[0], max2 = INT_MIN;
  int min1 = arr[0], min2 = INT_MAX;
  
  for (int i = 1; i < n; i++)
  {
    if (arr[i] > max1)
    {
      max2 = max1;
      max1 = arr[i];
    }
    else if (arr[i] > max2)
      max2 = arr[i];
    if (arr[i] < min1)
    {
      min2 = min1;
      min1 = arr[i];
    }
    else if (arr[i] < min2)
      min2 = arr[i];
  }
  if (max1 * max2 > min1 * min2)
    std::cout << max1 << ", " << max2 << std::endl;
  else
    std::cout << min1 << ", " << min2 << std::endl;
}

The algorithm is very straight-forward that the code itself is self explanatory.

Suppose we are given an unsorted array of integers and asked to find the pair of elements from the array that results in maximum product, how do we go about computing it?

A naïve approach is to find the product of each pair and maintain the maximum product seen so far. This would be an O(n^2) algorithm. Let us start with this and improve on it.

void maxprod(std::vector<int> arr)
{
  int n = arr.size();
  int max_prod = INT_MIN;
  int max_i, max_j;

  for (int i = 0; i < n-1; i++)
  {
    for (int j = i + 1; j < n; j++)
    {
      if (arr[i] * arr[j] > max_prod)
      {
        max_prod = arr[i] * arr[j];
        max_i = i;
        max_j = j;
      }
    }
  }
  std::cout << arr[max_i] << ", " << arr[max_j] << std::endl;
}

Can we do better than O(n^2)? Clearly, yes. We know that we could sort an array efficiently in O(n log n). We could sort the array and the maximum product would be either the product of the largest two elements or smallest two elements (if they are both negative).

void maxprod(std::vector<int> arr)
{
  int n = arr.size();
  std::sort(arr.begin(), arr.end());

  if (arr[0] * arr[1] > arr[n-1] * arr[n-2])
    std::cout << arr[0] << ", " << arr[1] << std::endl;
  else
    std::cout << arr[n-1] << ", " << arr[n-2] << std::endl;
}

Now, can we do better than O(n log n)?

In an earlier post, we saw how immutable objects like tuples are handled by Python’s memory management. It was straight-forward - tuples are immutable and so, when we try to update the tuple object, Python creates a new reference. Or does it? Always?

Let us consider the following tuple, this time a tuple of lists. Recall that lists in Python are mutable objects.

def mem_addr(item):
    return hex(id(item))

a = [1, 2]
b = [4, 5]
t = (a, b)
print(t)
print('memory referenced by t: {0}'.format(mem_addr(t)))

And our output:

([1, 2], [4, 5])
memory referenced by t: 0x2103c874a48

We see that the memory referenced by the object t which in our case is a tuple is 0x2103c874a48. And we know that tuples are immutable objects in Python. So, let’s try to change the above tuple object t. This time we are going to do that by updating the individual elements a and b that constitute our tuple object.

a.append(3)
b.append(6)
print(t)
print('memory referenced by t: {0}'.format(mem_addr(t)))

And we get the following printed:

([1, 2, 3], [4, 5, 6])
memory referenced by t: 0x2103c874a48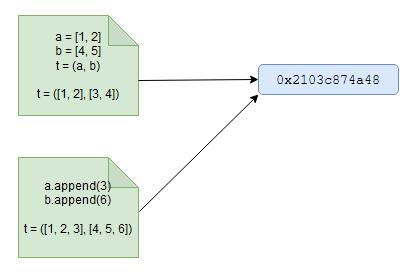

And what just happened here? Our immutable object t got updated without a new reference being created. So, it is not just the object itself that matters, the type of the constituent objects also plays a role in memory management. Hope this is enough motivation to play around with different mutable and immutable objects and how Python’s memory management handles them.