Keeping up with my modest goals from the previous post, I started looking at Google’s product portfolio.

• Why Google? - Why not?
• Why their product portfolio? - there is such a rich variety catering to different customer segments.
• Why for this topic (analysing how machine learning and/or deep learning will impact/improve the products)? - Because we already see the impact (like Google translate, maps, etc.)

Here’s their product portfolio, right from their webpage:

In future posts, we will pick products from this list and analyze.

I happened to complete an online course on Deep Learning and just starting to look at different products to see how machine learning or deep learning techniques could be used to make these products better. Since I understand technology products and their landscape better, I am likely to be biased in analysing more technology products than non-tech ones, although I am determined to study some non-tech industries, processes, products and services to see if (at all) and how deep learning could be used there - that is a bigger challenge and one that would stimulate our neurons more. Let’s see how I fare …

While driving back from a camping along with my friends and looking at the vast possibly burnt areas, we started thinking why even in the so called hot bed of technology (Silicon Valley) we hear that fire fighting aircrafts had visibility problems because of the dense smoke. Why can’t we use autonomous drone technology for fighting wild fires (given that we use unmanned drones for warfare). Something to think about seriously.

In the previous post we saw how to compute the length of the longest common subsequence (LCS). The algorithm returned an integer value indicating the length of the LCS. How do we go about extracting the LCS? With a simple extension to the previous algorithm, we can also extract the string sequence that is the LCS. In particular, we will traverse the populated lookup table and extract the LCS from that.

Let us consider a simple example, so that we can work it out by hand. Let the string s1 be ABCD and string s2 be BAD. Once we populate the lookup table as shown previously, it would look something like the one below

Populating the lookup table is the same as in our previous post, with just a reference to our lookup table passed to our function.

void lcs_dp(std::string s1, std::string s2, int m, int n,
            std::vector<std::vector<int>>& lookup)

Note that when either of the strings is empty, LCS is also empty and hence the length of the LCS is 0.

If one observes the LCS algorithm carefully, when a character of the strings match, in order to compute the value at (i, j) we look at the smaller subproblem (diagonally above and to the left - at coordinates (i-1, j-1) and add 1 to it.

if (s1[i-1] == s2[j-1])
  lookup[i][j] = lookup[i-1][j-1] + 1;

This tells us that if there is a match, the character in the string s1[m-1] (or s2[n-1]) would be a part of the LCS and hence we collect it in our result string and call our processing (the lookup table) function on the rest of the table, starting at (m-1, n-1).

If there is no match, then we compute the max of the subsequence lengths from (m-1, n) and (m, n-1). Potentially these could be two subsequences with the last character (that matched) the same.

else 
  lookup[i][j] = std::max(lookup[i-1][j], lookup[i][j-1]);

Essentially, for the value of the cell (i, j) we were computing the max of the values in the top cell (i-1, j) and the left cell (i, j-1). In order to extract the LCS, we hence need to move in the direction of the max (i.e. whether the current cell value was influenced by the top cell or the left cell).

Putting this together,

std::string get_lcs(std::string s1, std::string s2, 
                    int m, int n, 
                    std::vector<std::vector<int>>& lookup)
{
  if (m == 0 || n == 0)
    return std::string("");
  
  if (s1[m-1] == s2[n-1])
    return get_lcs(s1, s2, m-1, n-1, lookup) + s1[m-1];
  
  int top_cell = lookup[m-1][n];
  int left_cell = lookup[m][n-1];

  if (top_cell > left_cell)
    // go up
    return get_lcs(s1, s2, m-1, n, lookup);
  else
    // go left
    return get_lcs(s1, s2, m, n-1, lookup);
}

The traversal of the lookup table extracting the LCS ad is shown below:

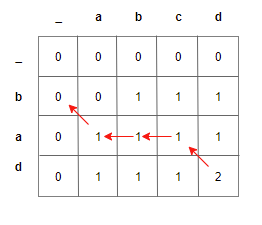
But LCS is not unique. There can be many LCS for a pair of strings. How do we collect all of the longest common subsequences?

LCS algorithm can also be implemented in a bottom-up fashion. That is, we can start from the simplest subproblem and build up the solution by progressively solving bigger problems. Instead of a hash-table we use a 2D array (2D as we would be tracking the lengths of sequences seen so far in the two input strings).

Suppose we are given two strings s1 and s2 of lengths m and n respectively. The base case corresponds to one of the strings being empty, in which case we do not have any common subsequence and just return 0.

int lookup[m+1][n+1];
for (int i = 0; i <= m; i++)
  lookup[i][0] = 0;
for (int j = 0; j <= n; j++)
  lookup[0][j] = 0;

We would use the above solutions (to the smallest subproblems) to progressively scan the two strings s1 and s2 looking which characters are matching, very similar to the approach seen previously.

Putting it together,

int lcs_dp(std::string s1, std::string s2, int m, int n)
{
  int lookup[m+1][n+1];

  for (int i = 0; i <= m; i++)
    lookup[i][0] = 0;
  for (int j = 0; j <= n; j++)
    lookup[0][j] = 0;

  for (int i = 1; i <= m; i++)
  {
    for (int j = 1; j <= n; j++)
    {
      if (s1[i-1] == s2[j-1])
        lookup[i][j] = lookup[i-1][j-1] + 1;
      else
        lookup[i][j] = std::max(lookup[i-1][j], lookup[i][j-1]);
    }
  }
  return lookup[m][n];
}