Many Large Language Model (LLM) APIs have certain parameters that help in selecting the tokens. I am not sure if these should be called parameters as these are unlike temperature, which is a hyperparameter - better considered as a sampling technique or inference time parameter setting. These control how predictable (i.e. one could be highly certain that the tokens would come from a most probable set of tokens) the output is. More technically, they control output probability distributions. After all, we are living in a world where probabilistic systems rule everything and everyone has, by now, heard of hallucinations from LLM applications that generate text.

Top-K

LLMs typically work on a sequence of tokens. For simplicity the tokens could be considered as words in the target language (for translation or content generation task). Note that most LLMs (like ChatGPT for example) tokenize on sub-words: i.e. for English language every word is approximately 1-1.5 tokens while for other European languages like Spanish or French every word is approximately 2+ tokens. It is important to note that the number is tokens is not the same as the number of words in the target language. When an LLM gobbles up an input sentence and tries to generate an output sentence, it has to predict the tokens in the output language vocabulary one by one. On a very high level, this generates a discrete probability distribution over all possible tokens available (the softmax layer at the end of your network does this). The different output tokens would have different probabilities associated with it and they would sum to 1.

For example, if our task is a sentence completion task, and our input sentence is

Aurore likes eating ____________.

Our LLM could potentially fill it up with any of the thousands of tokens that would have an associated high probability with eat. It could choose bread, cheese, pizza or even snail, rabbit or a shark. What if we want it to predict only the most likely outcomes (e.g. bread, cheese, etc. and not rare tokens like a shark), we can make the LLM choose from among the top K tokens. Our LLM would then:

Assume that there are only 6 tokens to choose from, with the following probabilities:

• Order all of the tokens in order of their probabilities
• Select the K tokens with the highest probablities and creates a new distribution
• Sample the token from this new distribution to predict

Note the the probabilities should add up to 1.

Now from the above set of six tokens, if we want to choose the most probable 3 tokens (K = 3), those would be:

This is our new distribution. However the probabilities should add up to 1 and hence the above set needs to be normalized by the sum of the K = 3 tokens. (0.43 + 0.35 + 0.16 = 0.94). This normalization would give us:

which sums to 1. If you set K=1, it would be a greedy approach where the highest probability token would always get selected.

Top-p

This is also referred to as nucleus sampling. Very similar to Top-K but instead of requesting certain most probable tokens, we want to choose enough tokens to cover a certain probability denoted p.

• Order all of the tokens in order of their probabilities
• Select the most probable tokens in such a way that their probabilities sum to at least p
• Sample the token from this new distribution to predict

Suppose we set p to 0.75 in our case, we would be picking the following tokens to choose from (their probabilities sum to at least 0.9 (0.43 + 0.35 = 0.78)

Again, we will have to normalize the new distribution as done in Top-K, so that the probabilities sum to 1.

The next time you feel hallucinated, you may want to check these parameter settings in your API calls.

The original motivation for using temperature to control the output of Large Language Models (LLMs) comes from Statistical Mechanics. This concept was adopted for neural networks probably first by David Ackley, Geoffrey Hinton and Terrence Sejnowskli in A Learning Algorithm for Botzmann Machines. While the paper talks about constraint satisfaction problems using a parallel network of processing units, the way to understand the concept of temperature for today’s neural networks is simpler.

Think of the neural network structure given below:

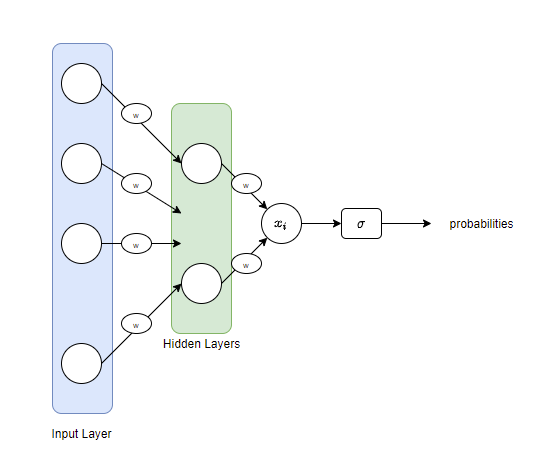
We have an Input layer, a set of hidden layers and also the activations shown by w (for multiplication by weight elements). What we get as an output is a real value $x_i$. If we are dealing with a binary classification task, what we want is to interpret this value $x_i$ to have two probabilities indicating the probabilities for the two possible classes. If our task is a multi-class classification, we will have more probabilities for outputs. A common choice for this is a sigmoid function, which for binary classification tasks is the logistic function and in multi-class tasks, the multinomial logistic function (softmax). This is the primary reason behind books referring to the arguments of softmax as logits. The term logit was originally used by Joseph Berkson to mean log of odds and as an analogy for probit.

Let’s understand it using some simple code fragments. In the below, we have some probabilities probs that add up to 1.

probs = [0.0001, 0.0179, 0.002, 0.03, 0.05, 0.4, 0.5]
probs, sum(probs)

> ([0.0001, 0.0179, 0.002, 0.03, 0.05, 0.4, 0.5], 1.0)

Let us calculate the log of the odds of these.

import math

def get_logits(probs):
  return [math.log(x/(1-x)) for x in probs]

logits = get_logits(probs)

logits

> [-9.21024036697585,
 -4.00489242331702,
 -6.212606095751519,
 -3.4760986898352733,
 -2.9444389791664403,
 -0.4054651081081643,
 0.0]

Let us compute the regular softmax function:

def softmax(logits):
    denominator = sum([math.exp(x) for x in logits])
    softmax = [math.exp(x)/denominator for x in logits]
    return softmax

And compute the softmax for our logits - essentially we are converting them into an interpretable way.

softmax(logits)

> [5.648507096749673e-05,
 0.010294080664302612,
 0.0011318521535150297,
 0.017467862616618552,
 0.029726011821263155,
 0.37652948306933326,
 0.5647942246039999]

Now, let us add the temperature parameter to control the softmax output. Our modified softmax is now:

def softmax_t(logits, t=1.0):
    denominator = sum([math.exp(x/t) for x in logits])
    softmax = [math.exp(x/t)/denominator for x in logits]
    return softmax

If we now compute softmax for different values of temperature (t in the function above),

softmax_t(logits, t=0.1)

> [9.83937567458523e-41,
 3.976549800632757e-18,
 1.0268990926840024e-27,
 7.870973150024767e-16,
 1.6032351163946892e-13,
 0.017045927454927112,
 0.9829540725449118]

For small temperature values t=0.1 for example, we see that the smaller logits almost vanish and the larger ones survive. If you think of these as tokens in the target language (a source-target language translation or content generation in a target language), it would mean that only a few of the tokens get a chance to be used and hence it would be relatively bland content.

If we increase the temperature, say to a 1 (t=1):

softmax_t(logits, t=1)

> [5.648507096749673e-05,
 0.010294080664302612,
 0.0011318521535150297,
 0.017467862616618552,
 0.029726011821263155,
 0.37652948306933326,
 0.5647942246039999]

If we keep increasing it to a 100, and then to a 1000, we see more interesting behaviors.

softmax_t(logits, t=100)

> [0.13520713120321545,
 0.14243152917854485,
 0.13932150536327115,
 0.14318669304928164,
 0.1439499862705803,
 0.14765163186672028,
 0.14825152306838635]

softmax_t(logits, t=1000)

> [0.14207868212056274,
 0.1428201792975013,
 0.14250522103172697,
 0.14289572168473877,
 0.1429717137819637,
 0.143335176443405,
 0.14339330564010144]

We see that more tokens are having similar chances of getting used. In the above case, at t=1000, every token has equal probability of getting used in the target language and hence it has more creative freedom to use all possible words and create more previously unseen (and some times awkward) content.

When a Deep Learning algorithm invented Halicin, there was instant speculation about the ability of Deep Learning algorithms to discover new knowledge which in this case was a new antibiotic compound. This compound also seemed to have a new structure that was different from existing antibiotic compounds. Does this constitute new knowledge? Of course, it does. After all, the structure of the compound was not known earlier. This is akin to solving a Sudoku puzzle by searching through an enormous search space and arriving at a solution. The solution is new knowledge - depending on the way you look at it.

While AI systems today are more akin to analogy machines than reasoning machines there is an intense debate about what kind of a machine would lead us to our quest of Artificial General Intelligence (AGI) - is the ability to reason needed at all? After all, human beings ourselves learn more through experiences and we reason more from our past experiences than from the rule book. However, according to Stanislas Dehaene’s book How We Learn we have certain intuition built into our brain that enables us to learn abstract concepts. In his book, he notes:

Characteristic of the human species is a relentless search for abstract rules, high-level conclusions that are extracted from a specific situation and subsequently tested on new observations … Learning means managing an internal hierarchy of rules and trying to infer the most general ones that summarize a whole series of observations.

This looks similar to logical reasoning (in the sense of mathematical logic in the realm of formal methods) where conclusions are inferred from hypotheses using a sequence of deduction rules. In order to illustrate this, let me pick one of the puzzles from TPTP library - the Aunt Agatha puzzle which is as follows:

Someone who lives in Dreadbury Mansion killed Aunt Agatha. Agatha, the butler, and Charles live in Dreadbury Mansion, and are the only people who live therein. A killer always hates his victim, and is never richer than his victim. Charles hates no one that Aunt Agatha hates. Agatha hates everyone except the butler. The butler hates everyone not richer than Aunt Agatha. The butler hates everyone Aunt Agatha hates. No one hates everyone. Agatha is not the butler. Therefore: Agatha killed herself.

If one were to encode the given facts in mathematical logic and prove the conclusion (the conjecture that Agatha killed herself) is deducible from the given facts, say in a theorem prover (like Vampire), it would be able to not only prove the conjecture, the logical reasoning system in Vampire would be able to show the sequence of steps that was used to arrive at the conclusion from the assumptions.

29. lives(sK0) [cnf transformation 26]
30. killed(sK0,agatha) [cnf transformation 26]
...
...
...
79. ~hates(butler,butler) [superposition 41,78]
...
...
82. hates(charles,agatha) <- (1) [backward demodulation 44,57]
89. ~hates(agatha,agatha) <- (1) [resolution 82,37]
...
...
93. $false [avatar sat refutation 66,71,81,92]

A Vampire proof run would also discover new knowledge (i.e. new facts not explicitly stated in our input set of facts). For example, it could deduce that the butler does not hate himself (line 79 above) which is not explicitly mentioned in the set of assumptions (derived from our natural natural language text). Such a kind of logical reasoning would be a great cornerstone for explainable AI systems of the future. However, languages themselves are ambiguous and translating from an ambiguous natural language into an unambiguous formulas in first order logic (as in this case) is not a trivial task. Maybe, just maybe one could generate such formulas themselves by training a model using a large corpus of natual language text and the corresponding logical formulas that would be able to capture the essence of natual language statements, context, etc. in logical form.

It was however not able to deduce new knowledge or to conclude if Agatha killed herself.

Note that the present day AI systems though demonstrate exemplary generative skills across text, images and video, the content generated, though novel in some cases, is an emergent behavior that arises from the vast knowledge base the model was trained on. Hence, it still lacks the capability to reason how it generated a particular content (it can not produce a sequence of deductions for example).

A symbiotic combination of logical reasoning and analogy based reasoning would enable both an efficient generation of impressive content while at the same time being able to reason about the chain of thought involved in the process. GreaseLM and LEGO are research efforts towards infusing reasoning capabilities in language models. They however work on pruning and traversing a knowledge graph based on the context from embedding vectors, rather than translating the knowledge into formulas in mathematical logic. AI systems that need to solve problems in mathematics and to derive new knowledge in the form of new mathematical proofs or conjectures would need more rigour and encoding the knowledge of mathematics in the form of logical formulas and training AI systems on such a corpus could be one way of achieving reasoning capabilities. Besides solving competitive math problems, such systems might be able to discover new physical structures that are lighter and stronger, or better algorithms that are currently unknown, better deterministic optimal algorithms in the place of present day heuristics, or even proofs of non-existence of better algorithms for certain problems.

The annotated logical encoding of the Aunt Agatha problem in TPTP syntax is provided below:

% axioms
% a1: someone who lives in D Mansion (DM) killed Agatha
fof(a1, axiom,
    ? [X] : (lives(X) & killed(X, agatha))).

% a2_0, a2_1, a2_2: Agatha, Butler and Charles live in DM
fof(a2_0, axiom,
    lives(agatha)).
fof(a2_1, axiom,
    lives(butler)).
fof(a2_2, axiom,
    lives(charles)).

% a3: Agatha, Butler and Charles are the only people who live in DM
fof(a3, axiom,
    ! [X] : (lives(X)
          => ( X = agatha
	     | X = butler
	     | X = charles))).

% a4: A killer always hates his victim
fof(a4, axiom,
    ! [X, Y] : ( killed(X, Y)
             =>  hates(X, Y))).

% a5: A killer is never richer than his victim
fof(a5, axiom,
    ! [X, Y] : ( killed(X, Y)
             =>  ~richer(X, Y))).

% a6: Charles hates no one that Aunt Agatha hates
fof(a6, axiom,
    ! [X] : ( hates(agatha, X)
          => ~hates(charles, X))).

% a7: Agatha hates everyone except the Butler
fof(a7, axiom,
    ! [X] : ( (X != butler)
          =>  hates(agatha, X))).

% a8: The Butler hates everyone not richer than Aunt Agatha
fof(a8, axiom,
    ! [X] : ( ~richer(X, agatha)
          => hates(butler, X))).

% a9: The Butler hates everyone Aunt Agatha hates
fof(a9, axiom,
    ! [X] : ( hates(agatha, X)
          =>  hates(butler, X))).

% a10: No one hates everyone
fof(a10, axiom,
    ! [X] : ? [Y] : ~hates(X, Y)).

% a11: Agatha is not the Butler
fof(a11, axiom,
   (agatha != butler)).

% c1: Agatha killed herself
fof(c1, conjecture,
    killed(agatha, agatha)).

The foundations for reasoning about computer algorithms predate the development of computer programming languages themselves. In fact, logic itself was developed in order to make arguments and discourse in natural language in a rigorous and structured manner so as to be able to reason about them. The word logic itself originates from the Greek word logos which could be loosely translated to reason, discourse or language and it involves the study of rules of thought or rules of reasoning. This allowed to deduce conclusions from a set of premises in a logical and structured way, removing many of the ambiguities. For a long time however, logic (in particular mathematical logic) was used to advance the field of programming languages - in particular to reason about the correctness of algorithms (erstwhile AI - symbolic AI or symbolic reasoning) given the various data structures provided by the different programming languages. When you think about it the tool (mathematical logic) that was developed to help in reasoning about natural languages made way to develop tools for more constrained language, with strict syntax and mostly strict semantics. In the last decade this has turned around and advances in algorithms, data and computation have enabled building systems that could understand natural language and attempt to reason about them.

We see two approaches to automated artificial intelligence:

1. Reasoning Engines: Based on rules or mathematical logic that allows one to reason about (give mathematical proofs) following rigorously established rules of mathematics and semantics of languages. This was the erstwhile AI that had several winters from 1950s to 1980s as data was expensive (there were no smartphone cameras) and computation was very expensive (there were no GPU data-centers).

2. Analogy Machines: Based on patterns seen in large amounts of similar data. The rise of inexpensive sensors (cameras) and proliferation of computing (smartphones) and internet enabled vast amount of data to pattern match (i.e. learn) from.

Is reasoning the core of intelligence as we usually think? Or would analogy machines turn out to be the Artificial General Intelligence (AGI) that everyone is racing for? Or would it be a powerful system that is able to automate several tasks and develop new impactful discoveries for mankind - like Halicin, but still not able to deduce everything that human minds are capable of? There is an intense ongoing debate between Computer Scientists, Philosophers, Neuroscientists, medical doctors, religious leaders and of course the general public about if the magnificient advancements in analogy machines, henceforth Deep Learning, one day lead to true AGI and what would positive and negative impacts of such a system be.

In a recent interview, Prof. Geoffrey Hinton a Turing award winning Computer Scientist claims that reasoning may not be the core of intelligence and that there are things similar to vectors in the brain that are just patterns of activities that interact with one another. This is similar to word embeddings in large language models (LLMs). There is a fantastic study about holographic memory by Prof. Karl Lashley who experimented with rats’ behavior in mazes and concluded that all information is stored everywhere in a distributed fashion and even if one part of the memory gets damaged one has access to all of the information.

Prof. Hinton contrasted symbolic reasoning and analogical reasoning and claimed that reasoning is easy when done using symbolic reasoning but perception is hard. It is hard to encode what we perceive into logical statements without introducing ambiguity. He claims that the reasoning employed by human beings is almost always analogical reasoning - reasoning by making analogies. Languages themselves are abstractions - they are just an approximate encoding for communicating our thoughts and not the actual representation of our thoughts. Hence different human beings might convey the same thought in different ways. The languages themselves as employed by us are just pointers to the vectors in our brain (similar to the weights in LLMs that point to embedding vectors).

It is quite likely we will get some kind of symbiosis. AI will make us far more competent. It is changing our view of what we are … it is changing people’s view from the idea that the essence of a person is a deliberate reasoning machine; the essence is much more a huge analogy machine … that seems far more like our real nature, than reasoning machines – Geoffrey Hinton

There used to be research interest in identifying which language constructs would make the best compiler or the best programming language and Computer scientists have looked at languages like Sanskrit to and deconstruct Panini’s rules.

However, languages themselves are not the same as are human thoughts and expressions of thoughts. Some languages have ways of expressing things that certain other languages do not. Some people have ways of articulating their thoughts that many others do not. Given this large variance, I am waiting to see how long before LLMs can become a more effective teacher or a more effective comedian.

I am also waiting to see what would be the best language for a machine to express thoughts would be - would it even be a textual language or would it be a visual one? Conversely what would be the best mode to communicate with an analogy machine be? How would you reason about what analogies it used to arrive at a prediction and in what sequence or order it used the analogies - much like a deductive reasoning engine for programming languages.

A few years ago, when Machine Learning was at its infancy, feature engineering used to be the swiss army knife for getting great results out of the models. Many domain experts, who claimed to know which features were important and which features weren’t important for a particular problem, became widely sought after. From a handful of features for predicting housing prices, like number of rooms, square footage, Zipcode, etc., to several hundreds of millions of features that might be present in a typical social media feed recommendation system, model features have grown at an impressive rate, thanks to the many varieties of inexpensive sensors and of course the distribution power of the internet. Feature Engineering became a role on its own in many companies that were building machine learning models. An automobile engineer would know which features are relevant or important to the stability of a car, while a grocery retailer would know about which items when placed at specific aisles in the store would garner more interest. Unsurprisingly, this also led to considerable interest from academia and subsequently there were more efficient techniques formalized and developed for effective feature selection based on the problem at hand and feature construction and feature extraction from raw data. Engineering teams started developing tools that facilitated such processes - like Featuretools for Python.

Fast forward a decade, feature engineering seems to be less in fashion while prompt engineering has captured the podium. This is primarily due to the interest and advancement in large language models. While earlier machine learning models were built to solve specific problems and hence needed domain experts to curate the features that best helps the model, advancements in few shot learning made selecting specific features less and less relevant while maintaining the same accuracy of the model. Today, models like OpenAI’s ChatGPT and the like can work on a variety of domains as they are trained on a collective dataset (dataset from as many different domains as possible) and hence have captured the relationships between the different domains by attaching weights to the learned contexts as did the previous machine learning algorithms that attached weights to different features. A word like teddy would be identified with a context of toys more (larger weights) while the data is about donations to charity for helping children. The same word however would be identified with a context of politics while the data is about national parks and national forests.

For example, experimenting with ChatGPT, when the system is prompted with the following question, it prompts back asking for clarifications, in order to identify the context.

user: Can you tell me about teddy?
ChatGPT: I'm sorry, but without additional context, I'm not sure which "teddy" you're referring to. 
There are several possible meanings for the word "teddy," such as:
...
...

The user might give an indirect context that the system still identifies with the initial prompt (teddy) - i.e. the system has memory and it retrieves the weights from its collection of different contexts, much like an indexing system would retrieve the best page among a collection of pages related to a search keyword.

user: tell me about the teddy related to national parks and forests
ChatGPT: Theodore Roosevelt is closely associated with the conservation movement in the United States and is often referred 
to as the "Conservation President." During his presidency from 1901 to 1909, he took significant steps to protect natural 
resources, establish national parks, and preserve wilderness areas.
...
...

The user could still prompt the system with a subsequent string that could entirely change the course of the conversation, much like how many real-world informal conversations move around from one topic to another while the topics themselves might be unrelated but tied together by some weak links.

user: tell me about the teddy related to donations to charity for children
ChatGPT: One possible "teddy" you might be referring to in this context is the "Teddy Bear" charity program. 
The Teddy Bear program is a charitable initiative that collects and distributes teddy bears and other stuffed animals 
to children in need, such as those who are sick, homeless, or traumatized.
The Teddy Bear program was first started by police officers in the United States in ...
...
...

The user could ask about an unrelated topic as a subsequent prompt but the system might still try to find a common context and if there is would talk about it, because the subsequent prompts are considered part of the same conversation.

user: what about fashion?
ChatGPT: In the world of fashion, a "teddy" can refer to a type of lingerie for women. A teddy is a 
one-piece garment that combines a camisole top and panties, often made from silk or other
...
...

Why is this impressive or important. In many real-world impactful applications (rather than informal chat systems), it is crucial to maintain a conversation topic - think about an airline customer service chatbot or an internet service center or education software where one builds on from simple fundamental concepts to advanced topics that are built by stitching together fundamental concepts. It is also crucial to have the ability to switch to a completely different topic even when there might be a related weak link in the conversation thread. This switch is effected by engineering the prompt in such a way as to turn the system’s attention from it’s current context to a new context.

user: No, let's just talk about contemporary fashion...
ChatGPT: Certainly! Contemporary fashion is a constantly evolving and diverse industry, encompassing a 
wide range of styles, trends, and designers. Some of the key trends and movements in ...
...
...

Now that prompt engineering gets the job done, is feature engineering irrelevant? Not really. It would still require a domain expert to help train the system with well engineered prompts in order for the system not to stray away. For example, a teacher could help with engineering the right prompts that would make the learning process more effective by not only charting the path to learn - from essential fundamental concepts to more involved concepts, but also in personalizing the path by identifying the learning challenges based on the questions (prompts) from the user (learner). This could be the next revolution in personalized, adaptive learning systems. There could be many other situations where such systems could benefit from domain experts. Some of them include negotiation systems, interviews and management training systems, navigation, technical support, as well as entertainment systems. Adding to this, multi-modal prompting systems, where the prompts themselves would have other modes (like voice, images, etc.) in addition to text would be immensely powerful in many real-world applications. Voice prompts would be very useful for autonomous machines, and image prompts would be exciting for content creation. I am eagerly looking forward to playing with those.